场论-张量

张量的基本概念与表示法

为什么要引入张量

为了描述物理定律（或物理量）不随坐标系的改变而改变就需引入张量，即参考系改变时，物理定律不变。

例如，要测P点温度，小明同学在P点t时刻测得P点温度为T，小红同学在相同时刻t，但在别处且相对小明同学有一个速度，测得P点温度为T*，那么T=T*必然成立。这说明温度T和参考系选取无关，因此温度是一个张量（零阶张量）。

又如，在P点有一个向量V，假设有两坐标系K与K*。在K坐标系下，向量为V；在K坐标系下,相同时刻，对同一向量测得其为V。那么V=V必然成立，因此V*为张量（一阶）。需注意的是，V与坐标系选择无关，但其各方向的分量与坐标系选择有关。

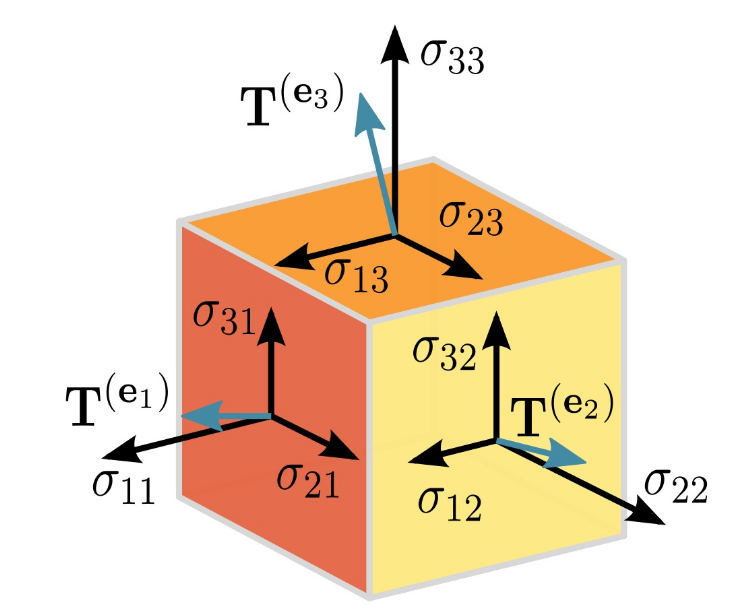
从上面我们可以看出，没有方向和有1个方向的量我们可以用常量与向量很好地描述，那么有2, 3, ... n个方向，且与坐标系选取无关的量应怎么描述？这就需引入n阶张量。如在连续介质力学中，要描述P点的应力状态，需同时指出应力作用方向与应力作用面的法向，因此应力仅用向量是无法描述的，需用二阶张量来描述。

什么是张量（Tensor）

张量是基于标量和矢量向更高维度的推广，它通过将一系列具有某种共同特征的数进行有序的组合来表示一个更加广义的“数“。其中，二阶张量在形式和性质上与二维矩阵有着高度的一致性，而在CFD中绝大多数情况下所涉及的也都是二阶张量，如笛卡尔坐标系下控制体单元所受到的黏性应力张量 $\tau_{ij}$ ：

$\tau_{ij}=\begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix}\\=\textbf{i}\textbf{i}\tau_{xx}+\textbf{i}\textbf{j}\tau_{xy}+\textbf{i}\textbf{k}\tau_{xz}+\textbf{j}\textbf{i}\tau_{yx}+\textbf{j}\textbf{j}\tau_{yy}+\textbf{j}\textbf{k}\tau_{yz}+\textbf{k}\textbf{i}\tau_{zx}+\textbf{k}\textbf{j}\tau_{zy}+\textbf{k}\textbf{k}\tau_{zz}$

可以看出，二阶张量有9个分量，而三阶张量有27个分量，更一般的，n阶张量有

张量的运算及矢量梯度、张量散度