像增强-对比度增强
# 图像增强技术
# 2 对比度增强——灰度变换
灰度变换可使图像动态范围增大,图像对比度扩展,图像变清晰,特征明显。
- 通过调整图像的灰度动态范围或调整图像的对比度进行图像增强;
- 对比度是指明暗的对比程度
# (1)全域线性变换
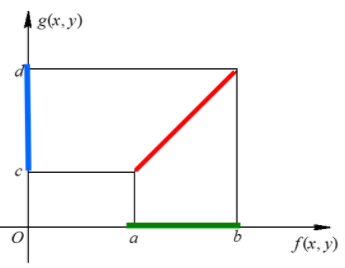
- f(i,j)→g(i,j),[a,b]→[c,d]
- g(i,j)=c+b−ad−c(f(i,j)−a)
- 应用在图片曝光不足或过曝的情况,图像灰度可能局限在一个很小的范围,可以进行__线性拉伸__。
反转变换:适于处理增强嵌入于图像暗色区域的白色或灰色细节,特别是当黑色面积占主导地位时。
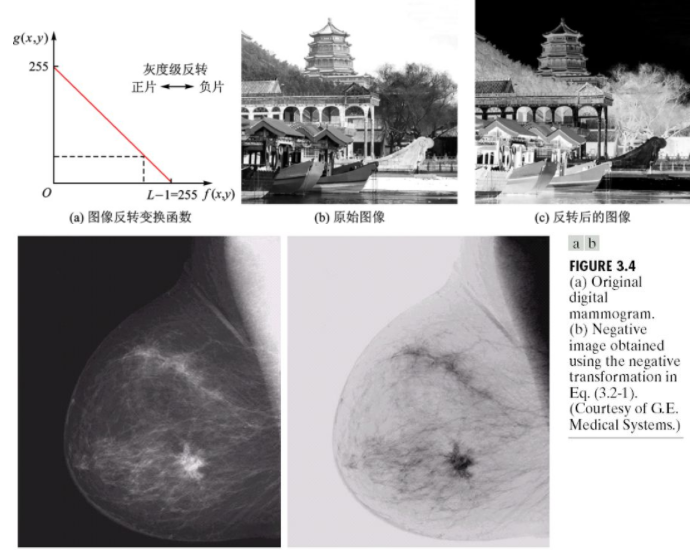
# (2)分段线性变换
- 如果只对图像中的部分目标感兴趣,这时候需要突出感兴趣目标所在的灰度区间,抑制不感兴趣的灰度区间,分段线性变换可以解决这类问题。
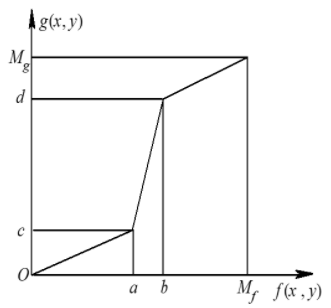
- f(i,j)∈[0,Mf],感兴趣的区间是[a,b],要把感兴趣的区间拉伸到[c,d],其中a>c>0,b<d<Mf.
- 若Mf==Mg,可见在[a,b]之间的像素点拉伸到[c,d],在[0,a)和(b,Mf]的像素点被压缩。
①灰度窗/开窗/削波处理
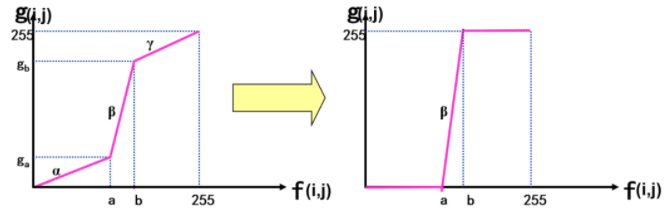

②灰度级分层(或是清除背景,或是保留背景)
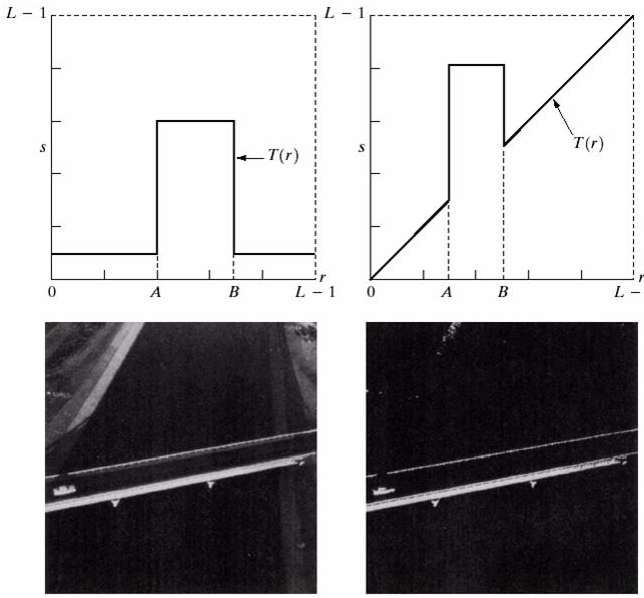
# (3)非线性灰度变换
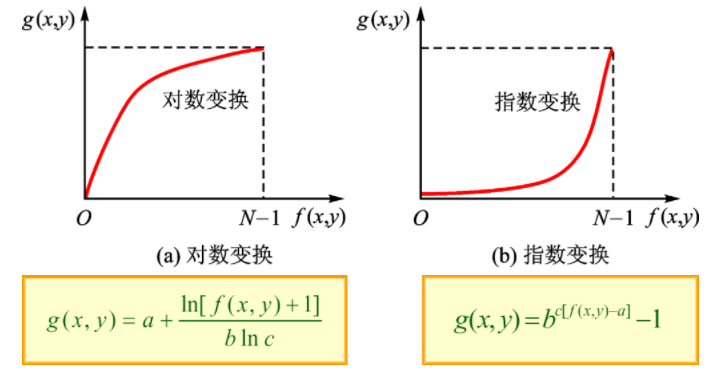
- ①对数变换:低灰度区扩展,高灰度区压缩。
- f(i,j)→g(i,j),[a,b]→[c,d]
- g(i,j)=a+blncln[f(i,j)+1]
- 在低灰度区有较大的拉伸,在高灰度取压缩。
- ②指数变换:高灰度区扩展,低灰度区压缩。使一窄带低灰度度输入图像映射为一宽带输出值,可以用于扩展被压缩的高值图像中的暗像素。
- f(i,j)→g(i,j),[a,b]→[c,d]
- g(i,j)=bc[f(i,j)−a]−1
- 在高灰度区有较大的拉伸
# 直方图处理
# 直方图的概念
- 灰度直方图:用来反应数字图像中每一个灰度级与这个灰度级出现频率之间的关系,可以描述图像的概貌。
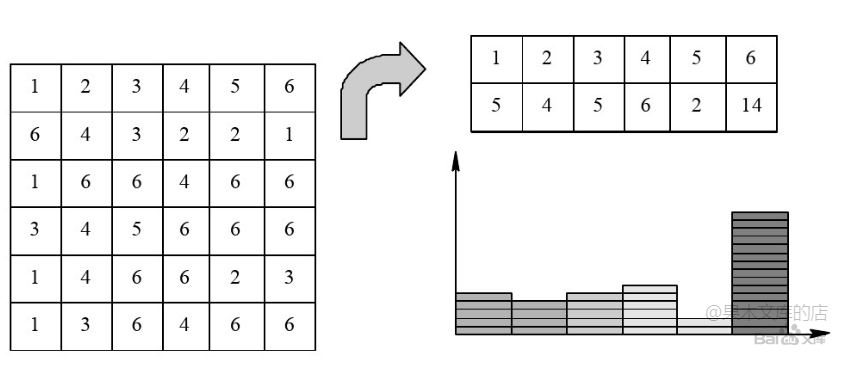
# 直方图修正法
- 直方图均衡化(主要讲解))
- 直方图规定化
# 3 对比度增强——直方图均衡化
- 概念:通过对原图像进行某种变换使原图像的灰度直方图修正为均匀的直方图,得到一副灰度直方图均匀分布的新图像,给人以色调协调的效果。
- 直方图均衡的实质是减少图像的灰度等级换取对比度的扩大。
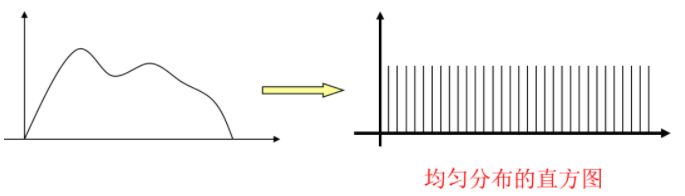

# 连续变化图像的均衡化问题
- 假设r表示归一化的原图像灰度,s表示经过直方图修正后的图像灰度.即
T(r)称为变换函数,需要满足以下条件:
- 条件1:在r∈[0,1]内,T(r)单调递增;
- 条件2:在r∈[0,1]内,有0≤T(r)≤1
条件1保证灰度级从黑到白的次序不变;
条件2保证映射后的像素灰度在允许的范围内.
则反变换关系为
- 显然,逆变换r=T−1(s)也满足上述条件1和条件2.
从概率论理论我们可以知道,如果已知随机变量r的概率密度为pr(r)而随机变量s是r的函数,则s的概率密度ps(s)可以由pr(r)求出
假定随机变量s的分布函数用Fs(s)表示,根据分布函数的定义,有(换个积分变量比较好,这里怕搞混直接用了)
利用密度函数是分布函数的导数的关系,等式两边对s求导,可以得到:
公式(一)是直方图修正级数的基础:可以通过变换函数T(r)控制原图像原图像灰度级的概率密度函数pr,得到输出图像的概率密度函数ps,因此可以改善原图像的灰度层次。
从人眼视觉特性来考虑,一副图像的直方图如果是均匀分布的,即Ps(s)=k(归一化后k=1),该图像色调给人的感觉比较协调。所以将原图像的直方图均衡化后,可以满足人眼的视觉要求.
如何求出T(r)
- 根据归一化假设
Ps(s)=1由公式(一)得到1=prdsdr,即:
ds=pr(r)dr两边同时求积分可以知道
s=T(r)=∫0rpr(r)dr(二)
所以,变换函数T(r)就是r的累计直方图函数。
- 将公式(二)推广到离散的数字图像,用频率代替概率,则变换函数T(rk)的离散形式可表示为:
- sk=T(rk)=∑j=0kpr(rj)=∑0knnj
- 这表明,均衡化后各像素的灰度值sk可直接由原图像的直方图计算出来.
# 实现步骤及计算
- 习题 如有一幅总像素为n=64×64=4096的图像,灰度级数为8,各灰度级分布列于表中。对其进行均衡化,计算过程如下:
| rk(归一化后的r取值) | nk | pr(rk)=nnk |
|---|---|---|
| r0=0 | 790 | 4096790=0.19 |
| r1=71 | 1023 | 40961023=0.25 |
| r2=72 | 850 | 4096850=0.21 |
| r3=73 | 659 | 4096659=0.16 |
| r4=74 | 329 | 4096329=0.08 |
| r5=75 | 245 | 4096245=0.06 |
| r6=76 | 122 | 4096122=0.03 |
| r7=1 | 81 | 409681=0.02 |
| r | rk(归一化后) | sk | 反归一化 | ps(k) |
|---|---|---|---|---|
| 0 | r0=0 | 0.19 | 1.33≈1 | ps(1)=4096790=0.19 |
| 1 | r1=71 | 0.19+0.25=0.44 | 3.08≈3 | ps(3)=40961023=0.25 |
| 2 | r2=72 | 0.44+0.21=0.65 | 4.55≈5 | ps(5)=4096850=0.21 |
| 3 | r3=73 | 0.65+0.16=0.81 | 5.67≈6 | ps(6)=4096659+329=0.24 |
| 4 | r4=74 | 0.81+0.08=0.89 | 6.23≈6 | - |
| 5 | r5=75 | 0.89+0.06=0.95 | 6.65≈7 | ps(7)=4096245+122+81=0.11 |
| 6 | r6=76 | 0.95+0.03=0.98 | 6.86≈7 | - |
| 7 | r7=1 | 0.98+0.02=1.00 | 7 | - |
变换后只有5个等级了,分别为1,3,5,6,7.
- 当原始图像的直方图不同而图像结构相同时,直方图均衡化所得到的结果在视觉上几乎是完全一致的.
- 从灰度直方图的意义上说,如果一幅图像的直方图非零范围占有所有可能的灰度级并在在这些灰度级上均匀分布,那么这幅图像的对比度较高,而且灰度色调较为丰富,从而容于判读.
# 4 对比度增强——直方图规定化
(精通Matlab数字图像处理与识别 张铮 Page63)
直方图均衡化__可以自动确定灰度变换函数,从而获得均有均匀直方图的输出图像,他主要用于__增强动态范围偏小的图像对比度,丰富图像的灰度级,这种方法的优点是操作简单,且结果可以预知,当图像需要__自动增强__时是一种不错的选择.
有时,我们希望对变换过程进行控制:如能够__人为地修正直方图的形状__,或者说是具有__指定直方图__的输出图像.这样就可以有选择地增强某个灰度范围内的对比度或使图像灰度值满足某种特定的分布.
这种用于产生具有特定直方图的图像的方法叫做:直方图规定化,或直方图匹配、
# 基本原理
理论基础:在运用均衡化原理的基础上,通过建立原始图像和期望图像(待匹配直方图的图像)之间的关系,使原始图像的直方图匹配特定的形状,从而弥补直方图不具备交互作用的特性。
- 使原图像灰度直方图变成规定形状的直方图。
- 直方图均衡化是直方图规定化的一个特例(均匀的直方图)。
# 实现步骤及计算
- 先对原始的图像进行均衡化
- 同时对待匹配直方图的图像进行均衡化处理
- 令s=v,可以得到
根据\tag{4-7}我们可以得到f(r),根据\tag{4-8}我们可以得到g(z),并且得到反函数g−1(z),对__原始输入图像??__应用\tag{4-9}公式进行变换,这样就执行了均衡化的逆处理.
直方图规定化本质一种拟合过程,因此变换得到的直方图与标准目标图像的直方图并不会完全一致,然而即使只是相似的拟合,仍然使得规定化后的图像在亮度与对比度上具有类似标准图像的特性,正是直方图规定化的目的.
-
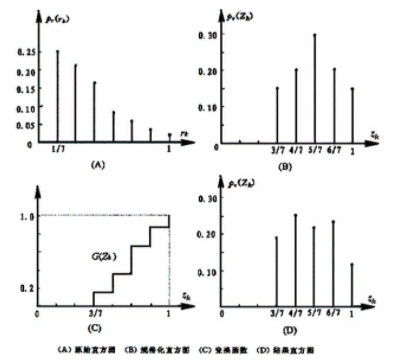
考虑一个64×64的假设图像,其直方图概率分布如下表第三列,希望直方图变换为下表第二列中规定的值.
Zq 规定的pz(Zq) 实际的pz(Zk) z0=0 0.00 0.00 z1=1 0.00 0.00 z2=2 0.00 0.00 z3=3 0.15 0.19 z4=4 0.20 0.25 z5=5 0.30 0.21 z6=6 0.20 0.24 z7=7 0.15 0.11 第一步对原始图像进行均衡化:
可以得到f(r)
f(r) pr(rk) r0=0 0.00 r1=1 0.19 r2=3 0.25 r3=5 0.21 r4=6 0.24 r5=7 0.11 第二步对目标直方图进行归一化
g(z=z0)g(z=z1)g(z=z2)g(z=z3)g(z=z4)g(z=z5)g(z=z6)g(z=z7)=10∗7=0=10+0∗7=0=10+0+0∗7=0=10+0+0+0.15∗7=1.05≈1=10+0+0+0.15+0.20∗7=2.45≈2=10+0+0+0.15+0.20+0.30∗7=4.55≈5=10+0+0+0.15+0.20+0.30+0.20∗7=5.95≈6=7对g(z)取反函数可以得到
g−1(z=0)g−1(z=1)g−1(z=2)g−1(z=5)g−1(z=6)g−1(z=7)=0,1,2=3=4=5=6=7根据v=g−1(f(r)),可以得到直方图规定化后的变换关系.
pr(rk) f(r) vc v 0.00 0 g−1(0)=0,1,2 0 0.19 1 g−1(1)=3 3 0.25 3 g−1(3)=??? 4 0.21 5 g−1(5)=5 5 0.24 6 g−1(6)=6 6 0.11 7 g−1(7)=7 7 对比一下规定化后的图像直方图分布和模板直方图.
Zk pz(zk) pv(vk) pr(rk) pz(Zq) 0 0.00 0.00 0.00 0.00 1 0.00 0.00 0.19 0.00 2 0.00 0.00 0.00 0.00 3 0.19 0.19 0.25 0.15 4 0.25 0.25 0.00 0.20 5 0.21 0.21 0.21 0.30 6 0.24 0.24 0.24 0.20 7 0.11 0.11 0.11 0.15
# 图书文献
MOOC《数字图像处理》——武汉大学——4. 图像增强


