边缘检测
边缘的定义
- 图像中像素灰度由阶跃变化或屋顶变换的那些像素的集合。
边缘的分类
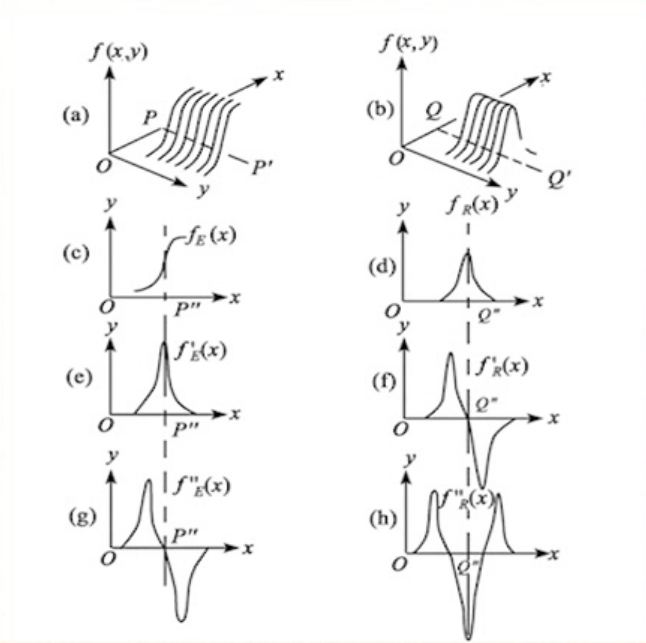
- 阶跃状:
- 灰度分布一维阶跃函数
- 一阶导数:在边缘处取到极值
- 二阶导数:在边缘处零交叉
- 屋顶状:
- 灰度分布正态状函数
- 一阶导数:在边缘处零交叉
- 二阶导数:在边缘处取到极值

边缘检测的代数理解
相关算子
梯度算子(水平垂直差分法)
函数f(x,y)在(x,y)处的梯度为一个向量
∇f=[∂x∂f,∂y∂f] 梯度大小为:
grad(x,y)=[(∂x∂f)2+(∂y∂f)2]21 也可以近似的表示为
grad(x,y)≈∣∂fx∣+∣∂fy∣grad(x,y)≈max(∣∂fx∣,∣∂fy∣); 梯度的方向为ϕ(x,y)=tan−1(∂fx∂fy)
梯度分量用模板表示为
[−1,1],[−1,1]T 为了检测边缘点,选取适当的阈值T,对梯度图像进行二值化,则形成了一幅边缘二值图像
g(x,y)={1,grad(x,y)≥T0,other - 特点:仅计算相邻像素的灰度差,对噪声比较敏感,无法抑制噪声的影响.
Roberts算子(45度角对角相差的梯度)
fx′=∣f(x+1,y+1)−f(x−1,y−1)∣fy′=∣f(x−1,y+1)−f(x+1,y−1)∣ PreWitt算子(3*3模板)
fx′=∣f(x+1,y−1)+f(x+1,y)+f(x+1,y+1)−f(x−1,y−1)−f(x−1,y)−f(x−1,y+1)∣fy′=∣f(x+1,y+1)+f(x,y+1)+f(x−1,y+1)−f(x−1,y−1)−f(x,y−1)−f(x+1,y−1)∣ ⎣⎢⎡−1−1−1000111⎦⎥⎤,⎣⎢⎡−101−101−101⎦⎥⎤, 特点:计算梯度的时候考虑了邻域的影响,在检测边缘的同时,能有效抑制噪声.
Sobel算子(带权邻域来计算梯度,四邻域的权值为2,八邻域的权值为1)
fx′=∣f(x+1,y−1)+2f(x+1,y)+f(x+1,y+1)−f(x−1,y−1)−2f(x−1,y)−f(x−1,y+1)∣fy′=∣f(x+1,y+1)+2f(x,y+1)+f(x−1,y+1)−f(x−1,y−1)−2f(x,y−1)−f(x+1,y−1)∣ ⎣⎢⎡−1−2−1000121⎦⎥⎤,⎣⎢⎡−101−202−101⎦⎥⎤, - 特点:对四领域采用带权方法计算差分,能进一步抑制噪声,但__检测到的边缘较宽__.
Kirsch算子(方向算子,夹角是4π)
- 方向模板(八个箭头方向,沿着箭头方向,左边为负,右边为正)
⎣⎢⎡−5−5−5303333⎦⎥⎤,⎣⎢⎡3−5−530−5333⎦⎥⎤,⎣⎢⎡33−530−533−5⎦⎥⎤,⎣⎢⎡33330−53−5−5⎦⎥⎤⎣⎢⎡333303−5−5−5⎦⎥⎤,⎣⎢⎡333−503−5−53⎦⎥⎤,⎣⎢⎡−533−503−533⎦⎥⎤,⎣⎢⎡−5−53−503333⎦⎥⎤ - 该方法用8个算子分别求卷积,取积和运算的最大值为边缘强度,而将与之对应的模板方向作为边缘方向
- 在计算边缘强度的同时可以得到边缘的方向,各方向间的夹角为4π.
Nevitia算子(和Kirsch算子类似,夹角是6π)
- 方向模板(一共该由十二个模板,就不一个一个抄了)
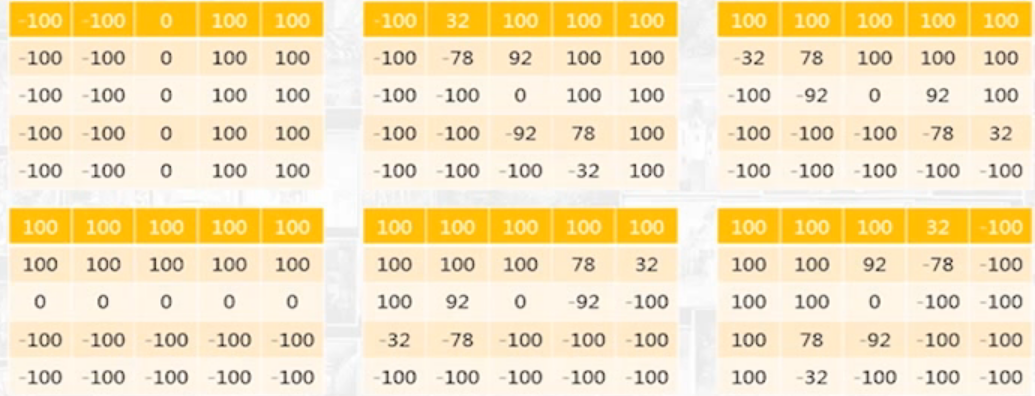
⎣⎢⎢⎢⎡−100−100−100−100−100−100−100−1000000100100100100100100100100⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡−100−100−100−100−78−100−100−100920−92−10010010078−32100100100100⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡−32−100−100−10078−92−100−1001000−100−10010092−78−10010010032100⎦⎥⎥⎥⎤... 拉普拉斯算子
∇2f=[∂x2∂2f,∂y2∂2f] ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y) 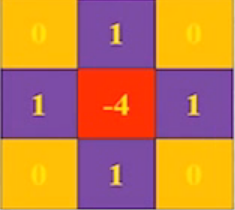
⎣⎢⎡0101−41010⎦⎥⎤ - 优点
- 各向同性,线性和位移不变的
- 对细线和孤立点检测效果较好;
- 缺点:
- 对噪声的敏感,对噪声由双倍加强作用
- 不能检测出边的方向
- 常产生双像素的边缘
由于梯度算子和拉普拉斯算子都对噪声敏感,因此一般在用他们检测边缘前要先对图像进行平滑。
由于拉普拉斯算子存在以上受噪音影响较大的缺陷,下面引入Marr算子
Marr算子(高斯+拉普拉斯算子)
- 由于拉普拉斯算子对噪声比较敏感,为了减少噪声影响,可先对图像进行平滑,然后再进行拉普拉斯算子检测边缘.
- 平滑函数采用正态分布的高斯函数,即
h(x,y)=e−2σ2x2+y2 - 用h(x,y)对图像f(x,y)的平滑可以表示为
g(x,y)=h(x,y)⋆f(x,y) 其中⋆表示卷积。令r是离原点的径向距离,即r2=x2+y2,对图像g(x,y)再采用拉普拉斯算子进行边缘检测.就可以得到
∇2g=∇2[h(x,y)⋆f(x,y)]=(−σ4r2−σ2)e−2σ2r2⋆f(x,y)=∇2h⋆f(x,y) 这样,利用二阶导数算子过零点的性质,可确定图像中阶跃边缘的位置.
- ∇h被称为高斯-拉普拉斯滤波算子,也被称为LoG滤波器,或者墨西哥草帽.
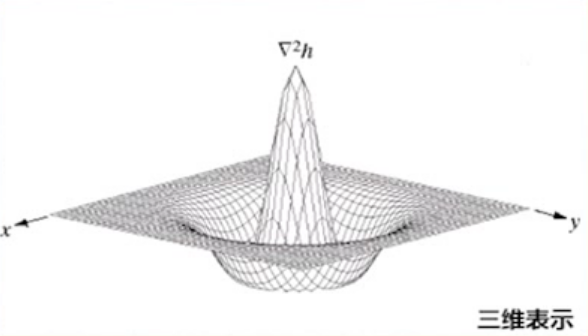
- 由于Marr算子的平滑性质能减少噪声,所以当边缘模糊或噪声较大时,利用Marr算子检测过零点提高可靠的边缘位置.
- 在该算子中σ的选择很重要,σ小时边缘精度高,但边缘细节变化多;σ大时平滑作用大,但细节损失大,边缘点定位精度低
- 应该根据噪声水平和边缘定位精度适当选择σ
- Marr算子的卷积模板一般较大,其半径一般为8 ~ 32.

曲面拟合法
出发点:基于差分检测图像边缘的算子往往对噪声敏感.因此对一些噪声比较严重的图像难以取得满意的效果.
若采用屏幕或高阶曲面来拟合图像中某一区域的灰度表明,求这个拟合平面或曲面外法方向的微分或二阶微分检测边缘,可减少噪声影响。
四点拟合灰度平面法:
- 若用一个平面p(x,y)=ax+by+c来拟合空间四邻像素的灰度值f(x,y),f(x,y+1),f(x+1,y),f(x+1,y+1),则均方差为:
ϵ=∑[p(x,y)−f(x,y)]2 - 按照均方差最小准则,可以求解参数a,b,c.经推导得到(好吧,直接抄下来).
2a2b4c=[f(x+1,y)+f(x+1,y+1)]−[f(x,y)+f(x,y+1)]=[f(x,y+1)+f(x+1,y+1)]−[f(x,y)+f(x+1,y)]=3f(x,y)+f(x+1,y)+f(x,y+1) [−11−11],[−1−111] - 按照梯度的定义,由平面p(x,y)=ax+by+c的偏导数很容易求得梯度,其近似表达式为
g(x,y)=∣a∣+∣b∣ 特点:
- 其过程是求平均后再求差分,因而对噪声有抑制作用.
- 用模板对图像求卷积进行边缘检测,计算a,b对应的模板为
21[−11−11],21[−1−111]
线的检测
- 通过比较模板的卷积和计算值,确定一个点是否正在某个方向上.
- 模板
⎣⎢⎡−12−1−12−1−12−1⎦⎥⎤,⎣⎢⎡−1−12−12−12−1−1⎦⎥⎤,⎣⎢⎡−1−1−1222−1−1−1⎦⎥⎤,⎣⎢⎡2−1−1−12−1−1−12⎦⎥⎤ - 我们通过计算四个模板的卷积结果,获取最大值是否大于某个门限,来判断是否是某种方向的线条。
图书文献
MOOC《数字图像处理》——武汉大学——7. 图像分割








