形态学处理-二值图像

• 二值图像处理的基本流程

二值图像处理的基本流程

二值图像的几何概念

主要关于二值图像的连接性和距离的相关概念

邻域和邻接

• 对于任意像素$(i,j)$,把像素的集合${(i+p,j+q)}$ ($p,q$是一对适当的整数) 叫做$(i,j)$的邻域.
• 直观上看，邻域就是$(i,j)$附近的像素形成的区域.
• 最经常采用的是$4$邻域(上下左右)和$8$邻域(上下左右,对角线)

像素的连接

• 对于二值图像中，若具有相同值的两个像素$A$和$B$,所有和$A$、$B$具有相同值的像素系列$p_0(=A),p_1,p_2,...,p_{n-1},p_n(=B)$存在且$p_{i-1}$和$p_i$互为$4/8$邻接,那么像素$A$和$B$叫做$4/8$连接,以上的像素序列叫做$4/8$路径.

连接成分(连通成分)

• 在二值图像中，把互相连接的像素的集合汇集为一组，于是具有若干个0值的像素($0$像素)和具有若干个1值的像素($1$像素)的组就产生了.

• 这些组就是连接成分或连通成分.

• 连接性矛盾示意图

  • 
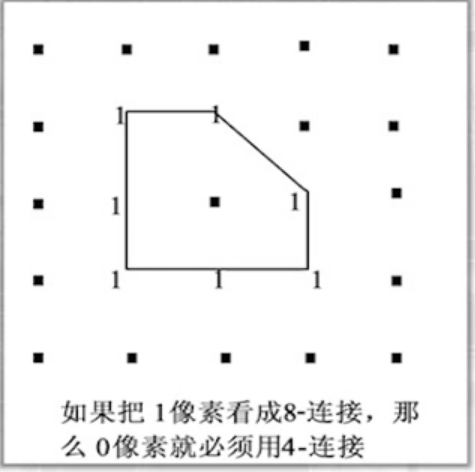
  • 如果把$1$像素看成8连接，那么$0$像素就必须用$4$连接.
  • 如果把$1$像素看成4连接，那么$0$像素就必须用8连接.

• 没有孔的连接成分称为：单重连接成分

• 具有孔的连接成分称为：多重连接成分

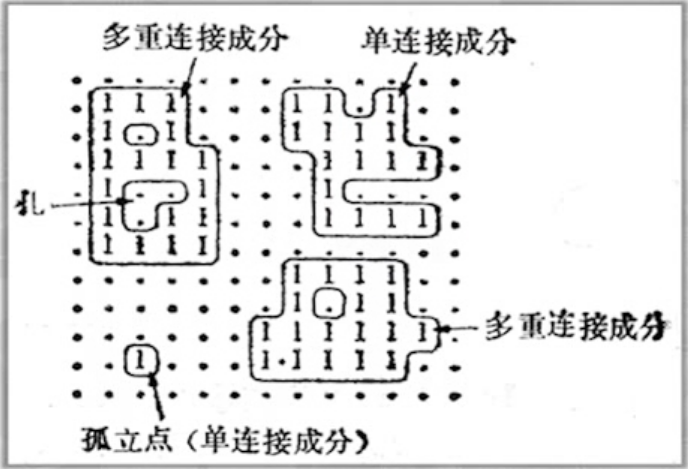
欧拉数

• 在二值图像中,$1$像素连接成分数$C$减去孔数$H$就叫做这幅图像的欧拉数或示性树.

$E = C-H$

• 对于一个$1$像素连接成分，$1$减去这个连接成分中所包含的孔数的插值就叫做这个$1$像素连接成分的欧拉数.
• 二值图像的欧拉数是所有$1$像素连接成分的欧拉数之和.

像素的可删除性和连接数

• 如果二值图像上的某个像素的值改变后,整个图像的连接性并不改变(各连接成分既不分离、不结合，孔也不产生、不消失),那么这个像素就是可删除的.
• 如何判断一个像素是否可删除?一般用像素的连接数来检测.
• 连接数：二值图像中某点$p$的像素值$B(p)=1$,则像素$p$的连接数$N_c(p)$为与$p$连接的连接成分数.
• 计算像素$p$的$4/8$邻接的连接数公式:

$N_c^4(p) = \sum_{k\in S}{[ B(p_k)-B(p_k)B(p_{k+1})B(p_{k+2}) ]}\\ N_c^8(p) = \sum_{k\in S}[\overline{B}(p_k)-\overline{B}(p_k)\overline{B}(p_{k+1})\overline{B}(p_{k+2})]$

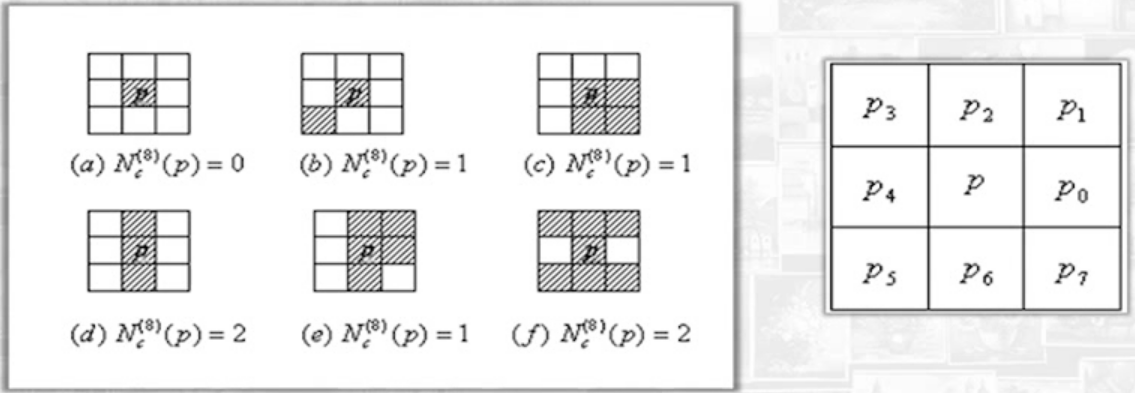
• 对于同一图像的像素，在$4$或$8$邻接的情况下，该像素的连接数不一定相同.
• 像素的连接数作为二值图像局部的特征量是很有用的.
• 像素按连接数$N_c(p)$的大小分类
  • 孤立点:对于$1$像素点$p$,在$4/8$邻接的情况下,当其$4/8$邻接的像素全是$0$时,像素$p$为孤立点.其连接数$N_c(p)=0$
  • 内部点:对于$1$像素点$p$,在$4/8$邻接的情况,当其$4/8$邻接的像素全是$1$时,称为内部点,内部点的连接数$N_c(p)=0$
  • 边界点:在$1$像素中, 除开孤立点和背景点$1 \le N_c(p)\le 4$.
    • 删除点或端点:$N_c(p)=1$;
    • 连接点:$N_c(p)=2$
    • 分支点:$N_c(p)=3$
    • 交叉点:$N_c(p)=4$
  • 背景点:把所有像素值$B(p)=0$的像素叫做背景点

	示例图
p1——孤立点 p2——内部点 p3-6——边界点 连接数1，2，3，4 p7——背景点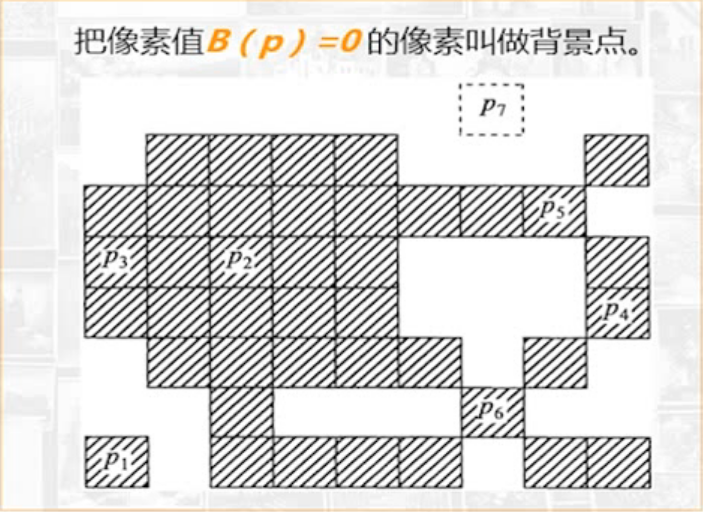

距离

• 对于集合$S$中的两个元素$p$和$q$,当函数$D(p,q)$满足下式时,就把$D(p,q)$叫做$p$和$q$的距离，也称为距离函数.

$\begin{cases} D(p,q)\gt 0 \\[2ex] D(p,q)=D(q,p)\\[2ex] D(p,r)\le D(p,q) + D(q,r) \end{cases}$

• 常用计算方法

欧几里得距离	4-邻域距离(街区距离)	8-邻域距离(棋盘距离、国际象棋)	八角形距离(结合$d_4$和$d_8$)
$d_e[(i,j),(h,k)] =\\ ((i-h)^2 + (j-k)^2)^{\frac{1}{2}}$	$d_4[(i,j),(h,k)] =\	i-h	+
大致圆形	倾斜45°正方形	正方形	八角形

• $d_8 \le d_4 \le d_e$

二值图像连接成分的各种变形算法

为了从二值图像中准确地提取有的特征，一般的需要对二值图像进行一些增强处理，这就是二值图像连接成分的变形操作

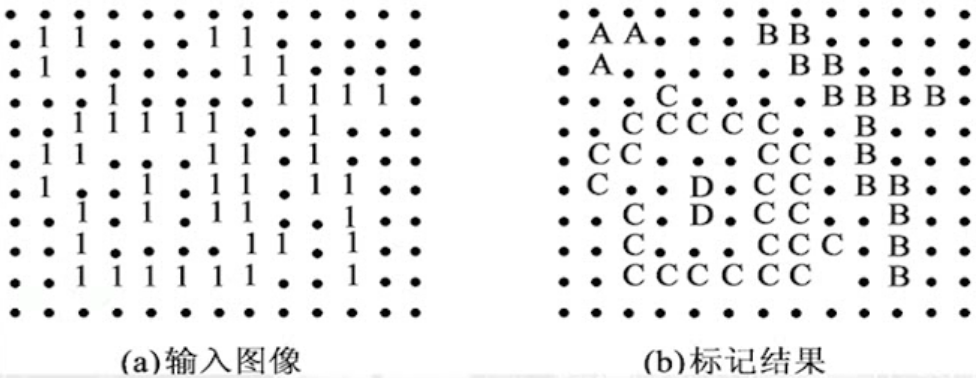
连接成分的标记

• 为了区分二值图像中的连接成分,求得连接成分的个数，对属于同一个$1$像素连接成分的所有像素分配相同的编号,不同的连接成分分配不同的编号的操作.

膨胀与收缩

膨胀	腐蚀
把连接成分的边界扩大一层的处理	把连接成分的边界点去掉而缩小一层的处理
$g(i,j) = \begin{cases}1,there\ is \ one\ '1'\ at \ last \in \ S_4\ or\ S_8 \\[2ex]0,other\end{cases}$	$g(i,j) = \begin{cases}0,there\ is \ one\ '0'\ at \ last \in \ S_4\ or\ S_8 \\[2ex]1,other\end{cases}$

膨胀和收缩的反复使用就可检测或清除二值图像中的小成分或孔

• 先膨胀后收缩:填平小沟,弥合空洞和裂缝.
• 先收缩后膨胀:去掉图中的孤立点的毛刺.

线图形化

• 距离变换和骨架化处理

  • 把任意图形转换成线划图的最有效方法之一.是求二值图像中各$1$像素到$0$像素的最短距离的一种处理.
  • 在经过距离变换得到的图像中，最大值点的集合就形成$1$像素区域的骨架.
  • 骨架反映了原图形的形状,给定距离和骨架就能恢复该图形，但恢复的图形不能保证原始图像的连接性。
  • 距离变换和骨架化处理常用于图像压缩、提取图形幅度和形状特征等.

• 

• 细化

  • 从二值图像中提取线宽为1的$1$像素的中心线的操作.

  • 从处理方法上分为顺序处理和并行处理,从连接性上分为8-邻接细化和4-邻接细化.

  • 介绍一种8-邻接细化中有代表性的一种方法-希尔迪奇(Hilditch)方法

    • 设像素$(i,j)$记为$p_0$,其8-邻域的像素用$p_k,k=1,2,3,4,5,6,7,8$表示 $$ \left[ \begin{matrix} p_4 & p_3 & p_2 \ p_5 & p_0 & p_1 \ p_6 & p_7 & p_8 \end{matrix} \right] $$

  • 二值图像的细化步骤

    1. 按光栅扫描顺序研究二值图像的像素$p_0$,当$p_0$完全满足以下六个条件时,把$p_0$的值$B(p_0)$置换成$-1$,注意,条件2、3和5是在并行处理方式中所用的各像素的值,条件4、6是在顺序方式中所有的各像素的值.
    2. 对已置换成$-1$的像素,在不用当前处理结果的并行处理方式中，把该像素的值复原到1，而在用当前处理的结果的顺序处理方式中，仍为-1.
    • 6个条件
      • 1. $p_0$的值必须等于1.
      • 2. $p_0$是边界像素的条件,即$\sum$
      • 这是在上你xx的课.

边界跟踪

• 为了求得区域间的连接关系，必须沿区域的边界点跟踪像素，这个过程称之为边界跟踪或边缘跟踪.

• 具体方法和步骤

  • 1. 根据光栅扫描发现像素从$0$开始变为$1$的像素$p_0$时,$p_0$作为边界的起点,存储他的坐标$(i,j)$值.
  • 2. 从像素$(i,j-1)$开始逆时针方向在像素$(i,j)$的8-邻域寻找$1$像素,当第一次出现$1$像素记为$p_k$,存储$p_k$的坐标.
  • 3. 逆时针方向从$p_{k-1}$以前的像素开始在$p_k$像素的8-邻域内寻找1像素，把最先发现像素值为1的像素记为$p_{k+1}$.
  • 4. 当$p_k=p_0$而且$p_{k+1}=p_1$时，跟踪结束，在其他情况下，把$k+1$重新当做$k$返回第$3$步,反复进行处理.
  

  $S_1$和$S_2$表示光栅扫描,$S_3$表示以$p_0$为中心逆时针扫描，$S_4$表示$p_1$为中心逆时针扫描,$S_5$表示以$p_2$为中心逆时针扫描,$S_6$表示以$p_3$为中心逆时针扫描.

• 二值图像的边界跟踪是在图像边缘连接明确的假设下进行的，但实际上很多图像的边缘连接并不是明显的.这时可以使用__浓淡图像直接跟踪边缘__,但必须同时进行边缘检出(根据图像斜率的大小和方向跟踪边缘的像素).

形状特征提取(区域内部形状提取与分析)

二值图像特征提取与描述的各种方法

• 对图像中的具体目标提取形状特征,进而对图像进行识别和理解.

• 提取方法

  • 区域内部形状特征提取

    • 空间域分析:直接在图像的空间域对区域内部提取形状特征，以便于分析.

      • 拓扑描述子:欧拉数,对区域的全局描述很有用.

      • 凹凸性:

        • 连接图形内任意两个像素的线段，如果不通过这个图像意外的像素，则这个图像就是凸的.
        • 包含一个图形的最小的凸图形称为这个图形的凸闭包，凸图形的凸闭包就是他本身.
        • 从凸闭包出去原始图形后，所产生的图像的位置和形状是形态特征分析的重要线索.

      • 区域的测量

        • 面积:区域的面积就是区域内像素点个数的总和
        • 周长
          • 第一种方法:在区域的边界像素中，设某像素与其上下左右像素间的距离为$1$，与斜方向像素间的距离为$\sqrt{2}$,周长就是这些像素间距离的总和.
          • 第二种方法:将边界的像素总和作为周长.
        • 圆形度:
        $R=4\pi\frac{面积}{(周长)^2}$

        如果区域为圆形,这时$R=1$,取得最大,如果区域为一个细长的区域,则$R$较小

        • 常用的特征量还有区域的__直径__、__幅宽__和__占有率__等.

    • 区域内部变换法:

      • 是形状分析的经典方法，包括求区域的__各阶统计矩__、__投影__和__截口__等.
      • 矩法:函数$f(x,y)$的$p+q$阶矩定义式为:
      $m_{pq}=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x^py^qf(x,y)dxdy \ \ \ p,q\in N_0 = \{0,1,2,... \}$

      则大小为$n\times m$的数字图像$f(i,j)$的矩为:

      $m_{pq}=\sum_{i=1}^{n}\sum_{j=1}^{m}i^pj^qf(i,j)$

      0阶矩$m_{00}$是图像灰度的总和,二值图像的$m_{00}$表示__对象物的面积__. 如果有$m_{00}$来归一化1阶原点矩阵$m_{10}$及$m_{01}$,则可以得到中心坐标$(i_G,j_G)$. $$ i_G = \frac{m_{10}}{m_{00}},j_G = \frac{m_{01}}{m_{00}} $$ 目标形心:是一个关键性的位置参数,它的精确与否直接影响到目标定位，可以用矩方法来确定. 定义中心距为: $$ M_{pq} = \sum_{i=1}^{n}\sum_{j=1}^{m} (i-i_G)^p(j-j_G)^qf(i,j) $$ 中心距能反映灰度相对于灰度中心是如何分布的. 利用中心矩可以提取一些区域的一些基本形状特征:延伸方向，对称轴. 艹xx的7个不变矩（Hu.M.K 对于平移、旋转和大小尺度变换均不变的矩组）

    归一化中心距定义式为: $$ \eta_{pq}=\frac{M_{pq}}{M_{00}^r}\ r = \frac{p+q}{2+1} $$ 求7个不变矩......

    7个不变矩在图像发生变化时，其数值基本保持不变。

    计算量较大,很少用.

    • 投影和截口

      • 对于区域为$n\times n$的二值图像$f(i,j)$,其在$i$轴上的投影 $$ p(i)=\sum_{j=1}^{n}f(i,j),i=1,2,...,n $$

      • 在$j$轴上的投影为： $$ p(j) = \sum_{i=1}^{n}f(i,j),j=1,2,...,n $$

      • 投影$p(i)$和$p(j)$都是__离散波形曲线__,这样把对二值图像的形状分析转化为对一维离散曲线的波形分析.

      • 如果我们固定$i$,假定为$i_0$,可得到图形$f(i,j)$过$i_0$而平行于$j$轴的截口$f(i_0,j),j=1,2,..,n$

      • 也可以固定$j_0$,可得到图形$f(i,j)$过$j_0$而平行于$i$轴的截口$f(i,j_0),i=1,2,...,n$

      • 截口函数所绘出的曲线也是两个一维离散波形曲线.

      • 二值图像的截口长度定义:

        $s(i_0) = \sum_{j=1}^{n}f(i_0,j)\\ s(j_0) = \sum_{i=1}^{n}f(i,j_0)$

      • 如果投影和截口都通过$f(i,j)$中的区域,那么上述的公示均是局域的__形态特征__.

      • 在分析染色体图像时,着丝点(凹点)位置是一个关键特征,用投影方法可以提取着丝点的位置.

  • 后面的没有找到视频提及.

  • 区域外部形状特征提取

    • ???

  • 利用图像层次型数据结构，提取形状特征(略).