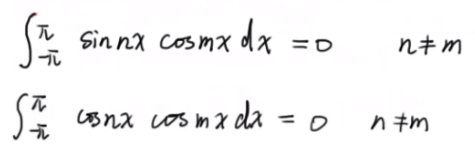傅里叶级数的三角函数形式
# 傅里叶级数的三角函数形式

# 无穷级数——傅里叶级数
# 傅里叶级数的目标
傅里叶级数目标是把周期函数f(x)展开为一个常数+一堆三角函数
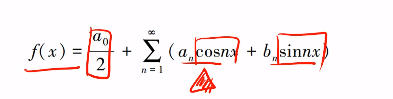
- 傅里叶变换赋予三角函数重要意义
- 既然周期函数都能展开为三角函数,那么三角函数即为周期函数的本原函数
- 它解释了高中和大学为什么要花费大量力气研究正余弦函数
- 可以说之前的这么多三角函数的学习都是为了傅里叶变换
上式的右端就是傅里叶级数的展开表达式。周期信号按照傅里叶级数展开,可以分解成为直流分量a0 ,和许多正余弦分量an,bn,而这些正余弦的分量必定是基频f1(1/T,T为周期函数的周期)的整数倍)。通常把频率为f1的分量称为基波,频率为2f1, 3f1,...等称为二次谐波、三次谐波...等。
# 知识基础
# 周期函数
# 周期函数的定义
简而言之,周期函数就是其定义域上的所有曲线会不断重复出现的函数,从数学的角度下一个定义即:在函数 f(x) 的定义域上有:
- f(x+T)=f(x)
其中,当 T>0 且取得 T = Tmin 使得上式成立时,称 T 为 f(x) 的最小正周期。
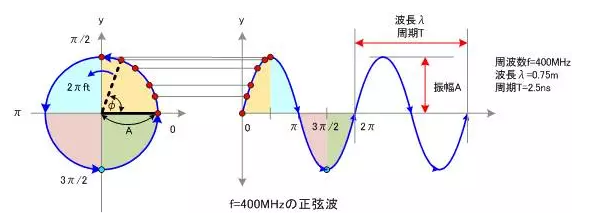
比如最典型的三角函数就是一个以 2 pi 为最小正周期的周期函数:
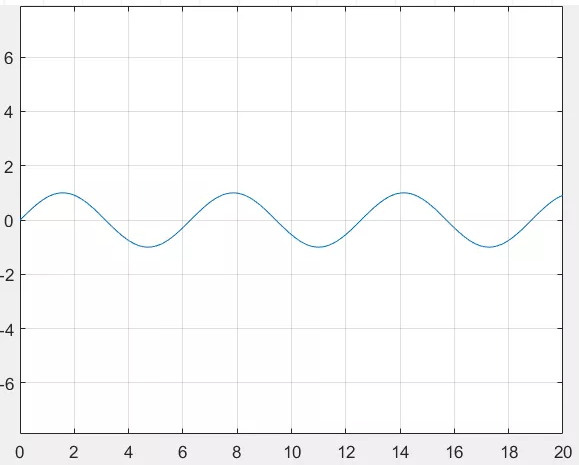
值得注意的是,周期函数要求上式都能在定义域上恒成立
- 比如这个函数,虽然其中绝大部分能重复出现,但上式并非恒成立,故也不是周期函数
# 三角函数系
“系”概念的引出
- 高中阶段我们就学习过直线系、圆系。
三角函数系
- 一个三角函数系:{0,1,sin(x),cos(x),sin(2x),cos(2x) ··· sin(nx) ,cos(nx) ··· ··· }称为三角函数系。
- 0——sin0x
- 1——cos0x
三角函数系的周期性
在这个系中,任意有限个项的和仍为周期为 2 pi 的周期函数。如下面这个函数:
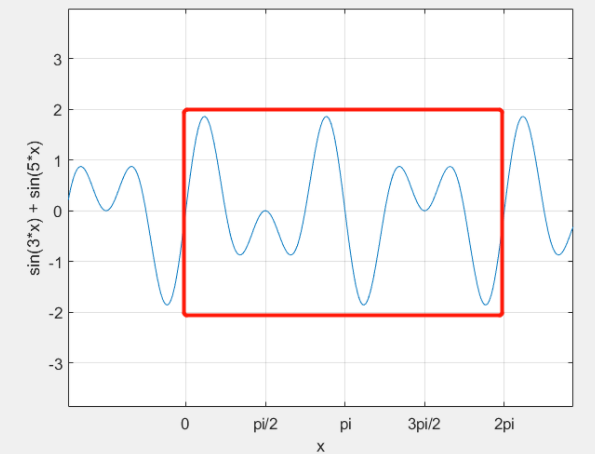
# 三角函数系的正交性(重点)
这是为下一步傅里叶级数展开时所用积分的准备知识。
任意取三角函数系中的两个函数,在一个周期内的乘积积分为零,形象的说就是垂直
正交(垂直) 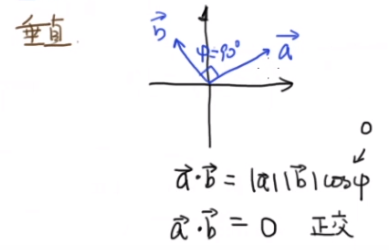
此处并不是说sinx和cosx垂直,这里是正交这个概念的引申了一下 利用三角函数——积化和差——可证得下式成立
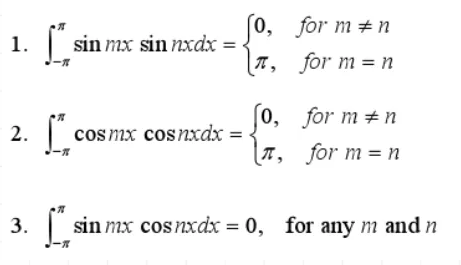
# 收敛定理
- 该定理又称为 Dirichlet 充分条件,由 Dirichlet 在1829年的论文《关于三角函数的收敛性》中整理并证明。
- 今天我们学习的内容中,已对 Dirichlet 充分条件进行了放宽。现在的 Dirichlet 充分条件如下:
- 函数 f(x) 周期为 2 pi ;
- 函数 f(x) 在 [ -pi , pi ] 上逐段光滑;
- 函数 f(x) 在 [ -pi , pi ] 上只有有限个极值点。
无法做傅里叶展开

# 傅里叶级数的基本原理
如同我们较为熟悉的泰勒展开一样,傅里叶级数展开也是一种函数展开。
将一个函数傅里叶展开时,我们选取的基底函数是
- 1,sin(x),cos(x),sin(2x),cos(2x) ··· sin(nx) ,cos(nx) ··· ···
为什么要将一个信号分解成这么多正弦信号的和呢?
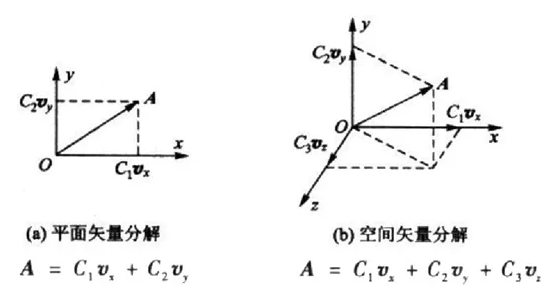
因为简单!
- 正如空间矢量分解,就是将某个向量一一映射到xyz三个方向上,只要三个方向正交就成。
- 而三角函数系也满足类似的正交性:三角函数系中任意两个不同的函数的积在一个周期上的积分为0。
- 由于正弦信号之间只有幅度、频率和相位的差别,因此信号表现的特性变得明显起来。
与泰勒级数不同的是,在傅里叶级数中,基底函数是正交的

因此我们说,傅里叶级数其实是一种正交分解。求系数的过程其实是在计算 目标函数在三角函数这种基底上的坐标。
# 傅立叶级数是向量
从代数上看,傅立叶级数就是通过三角函数和常数项来叠加逼近周期为 T的函数f(x):
f(x)=C+∑n=1∞(ancos(T2πnx)+bnsin(T2πnx))C∈R
该函数把f(x)当作了如下基的向量:
{1,cos(T2πnx),sin(T2πnx)}
那么上面的式子就可以解读为:
f(x)=基1下的坐标C+∑n=1∞(对应基的坐标ancos(T2πnx)+对应基的坐标bnsin(T2πnx))C∈R
说具体点,比如刚才提到的, T=2π 的方波 f(x),可以粗略的写作: $$ f(x) \approx 1 + \frac{4}{\pi} \sin(x) $$ 从几何上看,有那么一丁点相似:
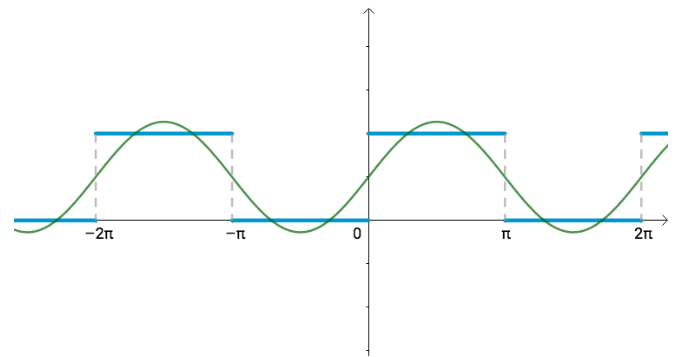
我们可以认为: $$ f(x) \approx 1 + \frac{4}{\pi} \sin(x) $$
此函数的基为:
$$
{ 1, \sin(x) }
$$
则f(x)相当于向量:
$$
{ 1, \frac{4}{\pi} }
$$
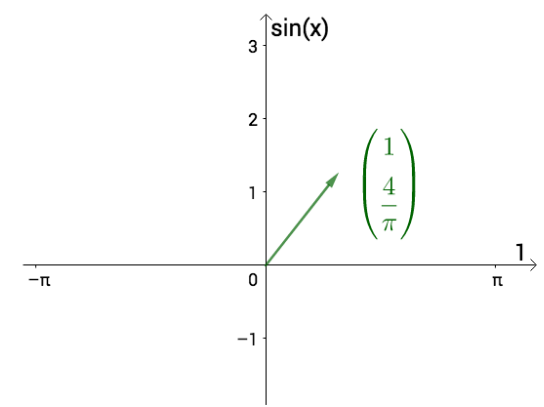
再增加几个三角函数:
从几何上看,肯定更接近了:
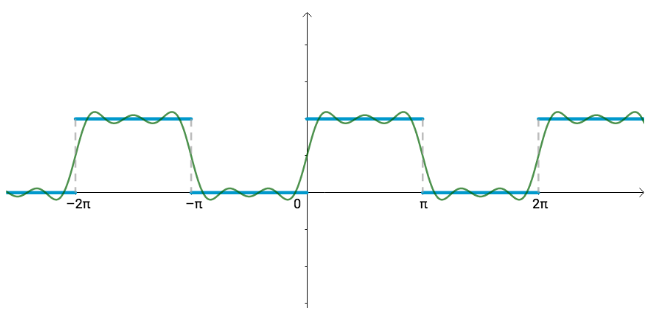
此时基为: $$ { 1, \sin(x), \sin(2x), \sin(3x), \sin(4x), \sin(5x) } $$ 对应的向量为: $$ { 1, \frac{4}{\pi}, 0, \frac{4}{3\pi}, 0, \frac{4}{5\pi} } $$ 六维的向量没有办法画图啊,没关系,数学家发明了一个频域图来表示这个向量:
| 频域图 | |
|---|---|
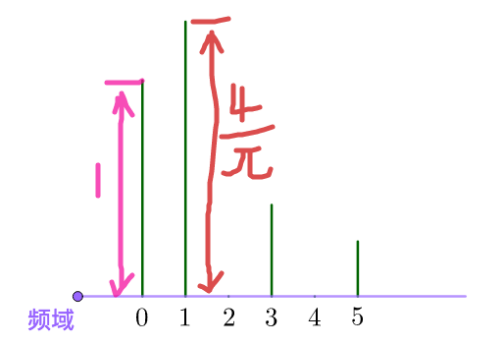 | 图中的1,2,3,4,5分别代表了不同频率的正弦波函数,也就是之前的基: 0Hz⇔sin(0x) 3Hz⇔sin(3x) 而高度则代表在这个频率上的振幅,也就是这个基上的坐标分量。 |
这里举的例子只有正弦函数,余弦函数其实也需要这样一个频谱图,也就是需要两个频谱图。当然还有别的办法,综合正弦和余弦。
# 正弦波作为频域的基本单元
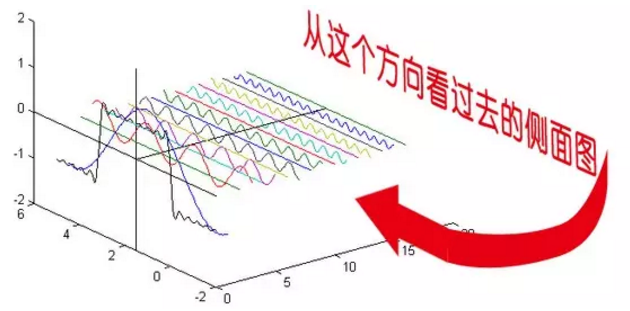
下面我们将正弦波累加成矩形波,换一个角度来看看:
| 正弦波累加成矩形波 | ||
|---|---|---|
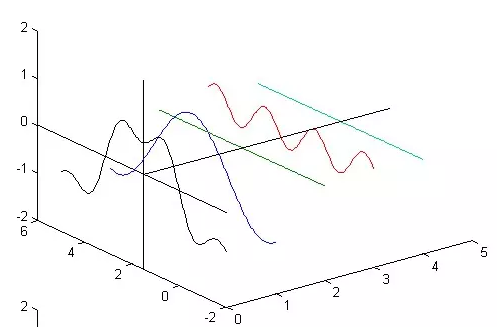 | 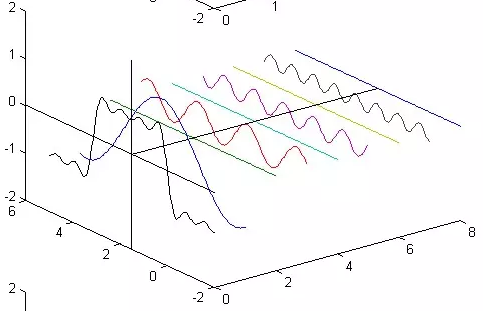 | 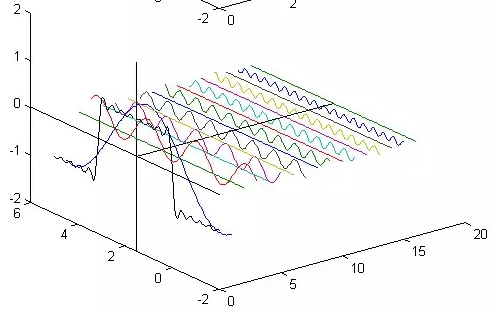 |
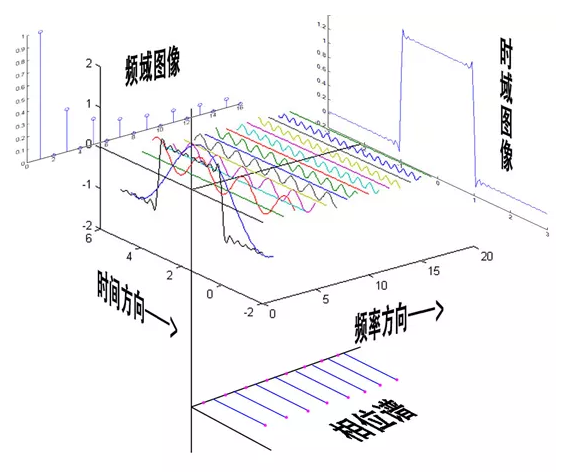
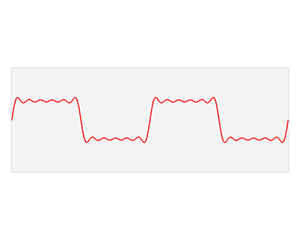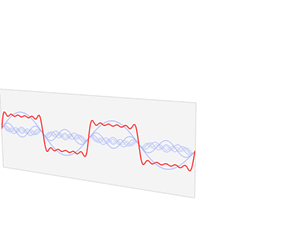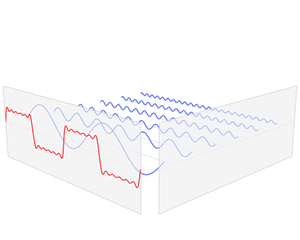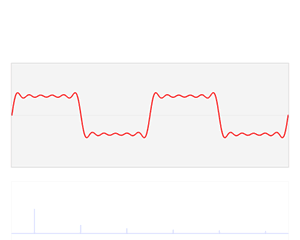
在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。
而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。
- 这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。
- 一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!
- 也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。
不同频率的正弦波我们称之为频率分量。
时域的基本单元就是“1 秒”,如果我们将一个角频率为ω的正弦波 cos(ωt)看作基础,那么频域的基本单元就是ω。
有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?
cos(0t)就是一个周期无限长的正弦波,也就是一条直线!
所以在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆。
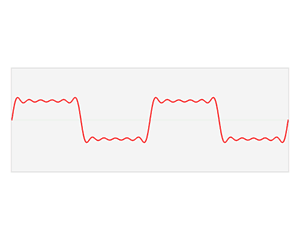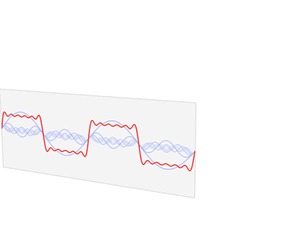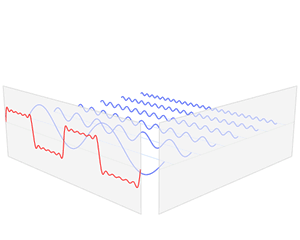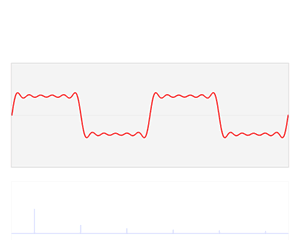
| 三角波的分解 | 方波的分解 |
|---|---|
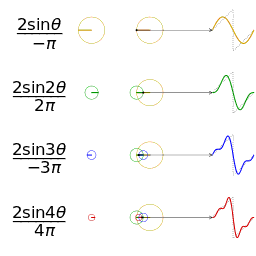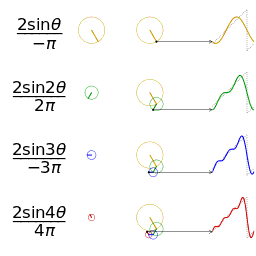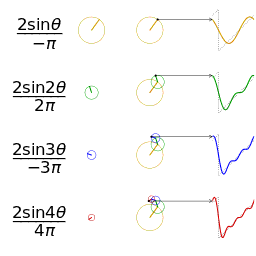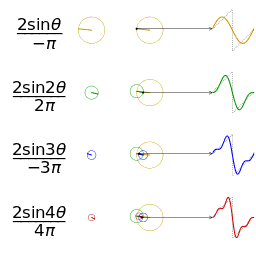 | 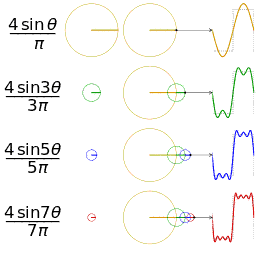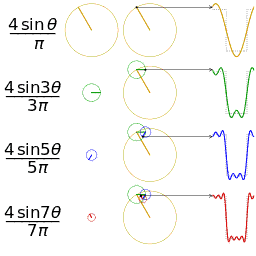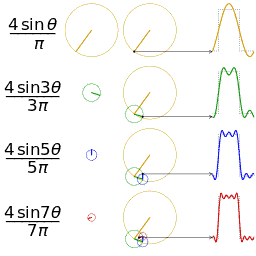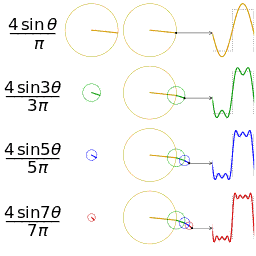 |
如上图,随着频率越来越丰富,合成的波形也越来越接近方波了,当n趋近于无穷大,也就是频谱范围无限大的时候,就可以无限逼近方波了。
但过冲不会降为零的。其实傅里叶所说的逼近其实是能量的无限逼近,也就是经过傅里叶变换后的波形能量和原始波形能量可以无限逼近。
介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样:
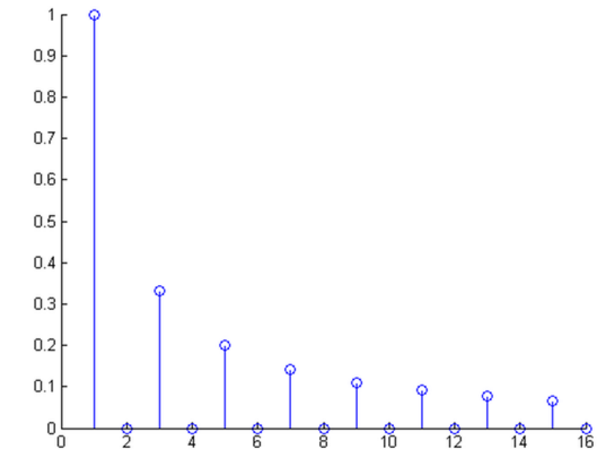
这是什么奇怪的东西?
这就是矩形波在频域的样子,是不是完全认不出来了?教科书一般就给到这里然后留给了读者无穷的遐想,以及无穷的吐槽,其实教科书只要补一张图就足够了:频域图像,也就是俗称的频谱,就是——
再清楚一点:
可以发现,在频谱中,偶数项的振幅都是 0,也就对应了图中的彩色直线。振幅为 0 的正弦波。
 |  |
想象一下,世界上每一个看似混乱的表象,实际都是一条时间轴上不规则的曲线,但实际这些曲线都是由这些无穷无尽的正弦波组成。我们看似不规律的事情反而是规律的正弦波在时域上的投影,而正弦波又是一个旋转的圆在直线上的投影。那么你的脑海中会产生一个什么画面呢?
我们眼中的世界就像皮影戏的大幕布,幕布的后面有无数的齿轮,大齿轮带动小齿轮,小齿轮再带动更小的。在最外面的小齿轮上有一个小人——那就是我们自己。我们只看到这个小人毫无规律的在幕布前表演,却无法预测他下一步会去哪。而幕布后面的齿轮却永远一直那样不停的旋转,永不停歇。这样说来有些宿命论的感觉。傅里叶级数思想……
# 傅里叶级数(Fourier Series)的相位谱
上一章的关键词是:从侧面看。这一章的关键词是:从下面看。
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。
- 因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。
- 基础的正弦波 A·sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。
- 那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用 7 个波叠加的图。
| 鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。 在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢? 为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。 当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。 | 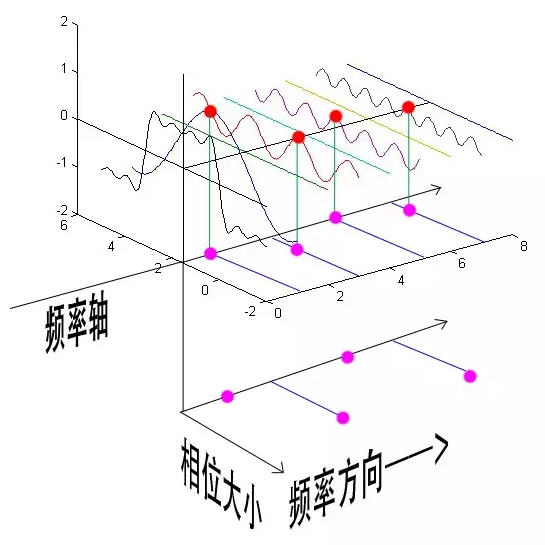 |
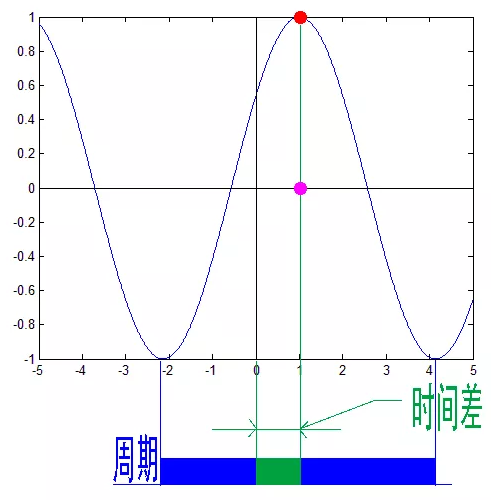
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作 2Pi 或者 360 度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘 2Pi,就得到了相位差
|  |
下次偷看女生裙底被发现的话,可以告诉她:“对不起,我只是想看看你的相位谱。”
注意到,相位谱中的相位除了 0,就是 Pi。因为 cos(t+π)=−cos(t),所以实际上相位为 Pi 的波只是上下翻转了而已。
对于周期方波的傅里叶级数,这样的相位谱已经是很简单的了。
另外值得注意的是,由于 cos(t+2Pi)=cos(t),所以相位差是周期的,pi 和 3pi,5pi,7pi 都是相同的相位。人为定义相位谱的值域为(-pi,pi],所以图中的相位差均为 Pi。
最后来一张大集合:

好了,你是不是觉得我们已经讲完傅里叶级数了?
抱歉让你失望了,以上我们讲解的只是傅里叶级数的三角函数形式。接下去才是最究极的傅里叶级数——指数形式傅里叶级数。
但是为了能更好的理解指数形式的傅里叶级数,我们还需要一个工具来帮忙——欧拉公式。
# 参考资料
http://www.jezzamon.com/fourier/zh-cn.html
https://www.bilibili.com/video/BV1c741127cy?from=search&seid=17844535962260850517