泰勒公式

# 泰勒公式(泰勒展开式)
泰勒展开,一个神奇而看起来颇为繁琐的公式,很多人初次看到的时候都会觉得头疼而麻烦,事实上,泰勒展开原本是非常美丽的。
# 高阶导数作用——泰勒公式引入
| 阶数 | 决定性 | 函数图示 | 比喻 |
|---|---|---|---|
| 一阶导数 | 单调性 | y=x | 吃穿 |
| 二阶导数 | 凹凸性 | y=x2 | 职业 |
| 三阶导数 | 在较宏观,较长远的地方影响函数曲线 | 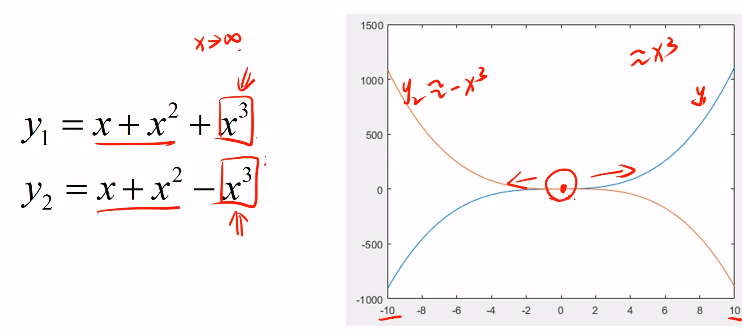 | 思想 |
| 四阶导数 | 在更加长远的地方影响函数曲线 | 文化背景 |
函数各阶导数之间的关系——代际关系

# 提出一个问题
如果所有阶导数都一样,那么两个函数的发展趋势完全一样,那么这两个函数就相等了
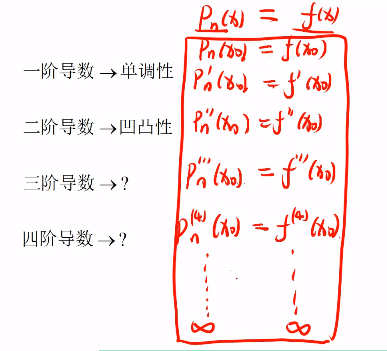
再形象一点,克隆一个人,在某一个时间点,将肉体,记忆,性格,习惯等等无穷多个要求都一样,就克隆完全一样的了,现在和未来都一样。这就是泰勒公式
如果只是满足前N项一样,那么就是展开到N项的泰勒公式。
如果满足无穷项的条件,那么就是泰勒级数。

这种用另一个函数无限逼近原函数的方式就是泰勒公式
# 从曲线拟合讲起
在讲解泰勒展开之前,需要了解一下曲线拟合。曲线拟合是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。
关于曲线拟合,首先是要有一推数据,然后就是构造一个曲线,使得已知的数据足够“符合”这条曲线。
这里的主要问题有两个:
- 如何判断曲线足够“符合”曲线?
- 一个简单的方法,就是把曲线构造出来,然后带入自变量,然后求已知数据和曲线上对应的数据点之间的均方根误差。
- 这里可以用最小二乘法进行求解,化为矩阵进行计算。
- 如何找到这条曲线?
- 如果我们能够知道这条曲线大概是一个什么线型的时候,问题会变得十分简单,只需要把这个具体形式带入进去,当然这其中包含几个我们需要求解的变量,这些变量通常用来调整x和y方向的缩放和平移。
但是很多情况下,我们无法预测曲线的线型。那怎么办呢,有没有通用的一个线型的形式呢?或者说能够构造一个通用线型使得其在很大程度上能够与任何一个曲线无限相似?
答案是肯定的,那就是多项式的线性
至于这个函数为什么可以与任意一条曲线无限相似
- 事实上很难证明,通俗的理解可以认为是这个展开可以有无穷项
- 总是能找到一组系数 an 使得跟我们所需要的曲线足够接近
- 这就像神经网络能够模拟所有的函数,如果模拟的不好,那就加更多的层数。
当然,并不是说展开的阶数越多就越好,因为毕竟数据本身可能带有误差,如果完全“符合”上了,反而使得结果不正确了,这就是神经网络里说的过拟合问题。当然这就有点扯远了。
回到主题,接下来要介绍泰勒展开了。
# 什么是泰勒公式?
要学习泰勒公式我们先要知道泰勒是一个数学家的名字,“布鲁克,泰勒”18世纪初英国有名的大数学家,泰勒公式就是以他的名字命名。
泰勒公式,也称泰勒展开式。
# 泰勒展开式究竟要做的是什么?
泰勒展开一句话描述:就是用多项式函数去逼近光滑函数。
细胞,分子,原子,中子,似乎这个世界只要你无限细分就能得到组成这个世界的统一的基本单位。
而泰勒公式要做的就是将所有的可导函数统一的形式表达出来。
本质上就是为了在某个点附近,用多项式函数取近似其他函数。
可能有些童鞋就要问了,既然有一个函数了,为什么还需要用多项式函数取进行近似
理由就是多项式函数具有非常多优良的性质
- 比如说,多项式函数既好计算,也好求导,还好积分,等等一系列的优良性质。
很多特殊类型的函数无法快速求值,比较讨厌
- 三角函数
- e的函数
- 这类函数能不能用多项式进行表达呢
这就是泰勒展开的出发点
我们已经知道了它的用途是求一个函数的近似值。
之前提到了曲线拟合是知道一推数据,得到其曲线。试想一下,如果只有一个点 x0 的数据,或者说,只知道这个点附近一小块区域的数据,如何去拟合得到一条曲线?
之前已经说过,用多项式拟合原则上可以与任何一个曲线无限相似,用同样的方法。
但是我们怎么来求呢,其实一个比较朴素的思路是通过斜率逼近。
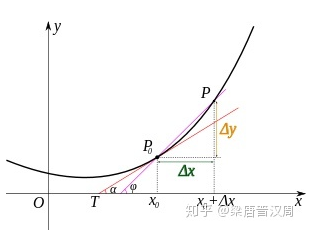
# 泰勒展开的核心思想
要实现近似,就要求所有以下物理量,其变化率要相同!
如果两条曲线想要在某一点上完全一样,那么它们在某一点的一阶,二阶···N阶都相同

# 要如何做到?显然有表达式F(x)=f(x)
那么:
- 首先要求两曲线在(x0,f(x0))点相交
- 如果要靠得更近,还要求两曲线在(x0,f(x0))点相切
- 如果还要靠得更近,还要求曲线在(x0,f(x0))点弯曲方向相同
| 泰勒公式:逼近与克隆人 | |
|---|---|
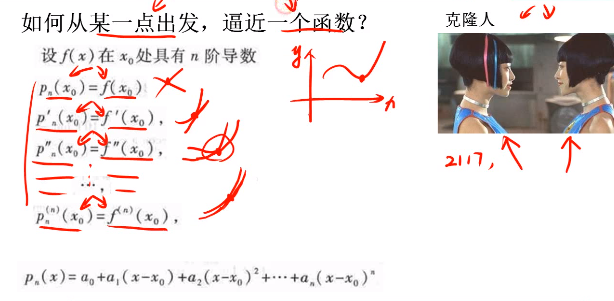 | 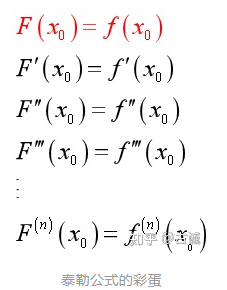 |
 | 使用幂函数取拼凑一个逼近函数 因为幂函数有特殊的性质: 每一个幂函数只有一个阶层的导数不为零 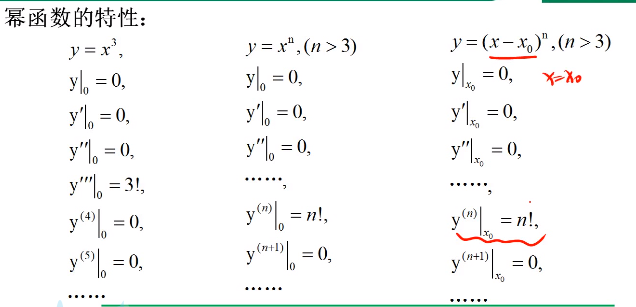 |
 | 可以通过获得幂函数的每一阶的导数值 来非常近似的把f(x)还原出来。 好比用一个女孩的某个时刻的所有信息 就能完美的克隆出来一个非常近似的女孩 获得某一点的信息就能把整个函数还原 类似于函数的DNA |
这就需要目标函数具有无限可导,逼近函数为幂函数
- 恰好,sinx ex具有无限可导的特性
总而言之,逼近函数就是依赖微分,从而实现无限逼近。
# 泰勒公式作图理解
下面我们通过作图来进一步理解泰勒公式
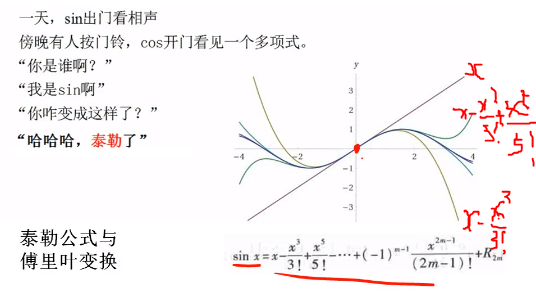
注意:这里是在零点用幂函数去逼近sinx,所以只有在零点这个幂函数叠加是最接近sinx的,而在越远离零点,误差越明显。
- 因此在用泰勒公式的时候,通常是帮我们研究原函数在这一点的性质,而不是研究原函数整个函数曲线的性质
- 因为这个展开式只有在这个点附近逼近的非常好,远离展开点就没有那么近似了
- 原则上,只有把这个幂函数展开到无穷阶的时候,这些叠加才完全和原函数一样。
- 但通常我们都是有限阶展开。
- 好比在某个点进行克隆的人,和自然人,只有在那一点完全一致,附近人生轨迹近似,随着时间越久,人生轨迹差异越来越大。因为克隆能力有限,哈哈😄
ex也是一样
在0点进行泰勒展开后的函数可以用来研究原函数在x=0的位置的性质,而其他位置是有误差的。
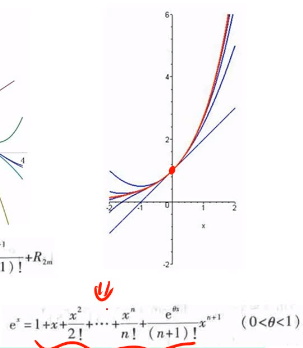
由此可知,泰勒公式存在一个问题,就是我们只能知道一个点的数据。也就是:
要研究哪一个点的性质,我们就把原函数在哪个点进行泰勒展开
# 泰勒展开的阶数(展开几项)
在多项式拟合中,并不是阶数越多越好,因为会带来过拟合的问题。那么在泰勒展开中,展开阶数越高又会产生怎样的影响呢?
首先要明确一点,在之前的推导中,我们只是知道一个邻域的数据,但是这个邻域有多大呢?事实上,在泰勒展开中,越高的阶数表示所知道的这个邻域越大。
非常容易理解的一件事
- 如果我告诉你一个运动者的人在某一时刻的位置,但是下一秒的位置,实际上不知道的。
- 那么如果我再告诉你这一时刻这个人的速度,你基本可以判断下一个时刻这个人的位置。但是你依然无法判断更长的时间之后这个人的位置。
- 那么我再告诉你这个时刻的加速度,那么你所能判断更长时间的位置。速度是距离的一阶导数,加速度是二阶导数。
- 泰勒公式——微分处理
- 傅里叶变换——积分处理
# 泰勒展开余项
| 泰勒展开的余项表示方式:拉格朗日型余项,皮亚诺型余项 | |
|---|---|
 |  |
| 如果取x0=0,则成为麦克劳林公式 |
# 常见泰勒公式
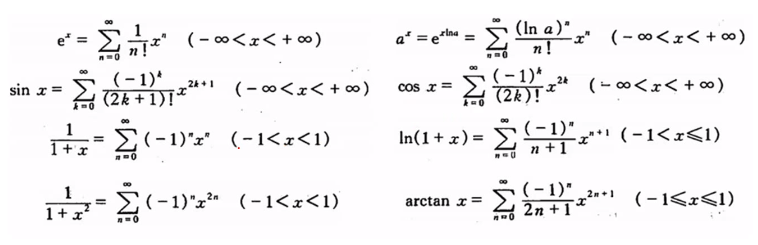

https://www.bilibili.com/video/BV1Gb411L7PM?p=2
https://www.bilibili.com/video/BV1Jx411s7Qe?p=1



