傅里叶变换

# 从傅里叶级数到傅里叶变换
在《傅里叶分析》中,一开始关于钢琴琴谱的例子其实是一个公式错误,但是概念典型的例子。所谓的公式错误在哪里呢?
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。
在这个世界上,有的事情一期一会,永不再来,并且时间始终不曾停息地将那些刻骨铭心的往昔连续的标记在时间点上。
但是这些事情往往又成为了我们格外宝贵的回忆,在我们大脑里隔一段时间就会周期性的蹦出来一下,可惜这些回忆都是零散的片段,往往只有最幸福的回忆,而平淡的回忆则逐渐被我们忘却。
因为,往昔是一个连续的非周期信号,而回忆是一个周期离散信号。
是否有一种数学工具将连续非周期信号变换为周期离散信号呢?
抱歉,真没有。
比如之前说的傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。

# 傅里叶变换
那么既然傅里叶级数只对周期信号有用,那么非周期信号怎么办?
非周期函数,比如下面这个函数可以写出傅立叶级数吗?
这并非一个周期函数,没有办法写出傅立叶级数。
不过可以变换一下思维,如果刚才的方波的周期: $$ \Large T = 2\pi \Rightarrow T = \infty $$ 那么就得到了这个函数:
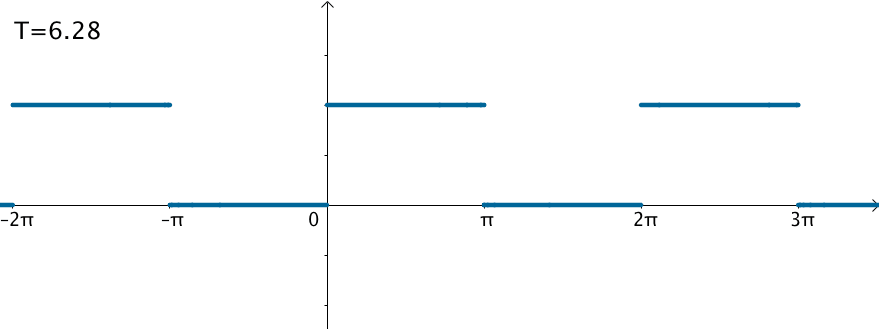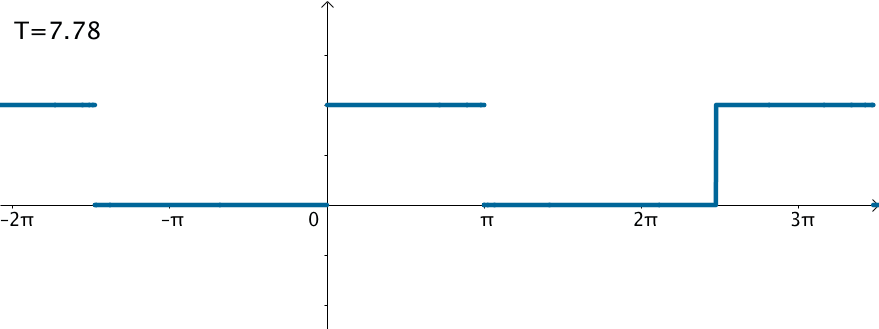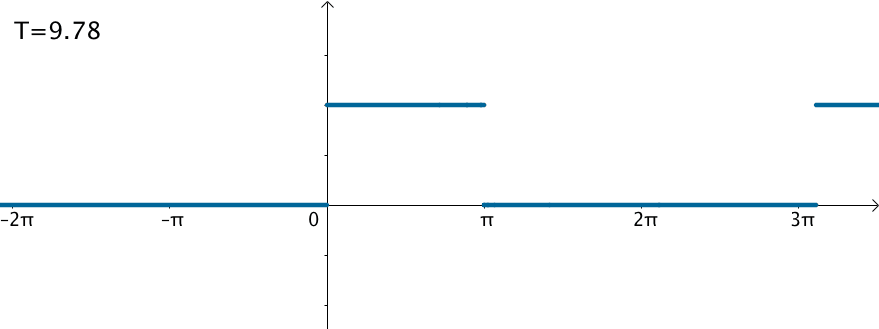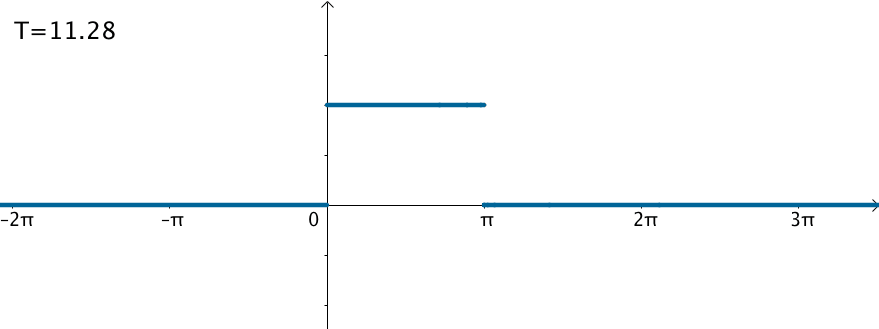
在这样的思路下,就可以使用三角级数来逼近这个函数:
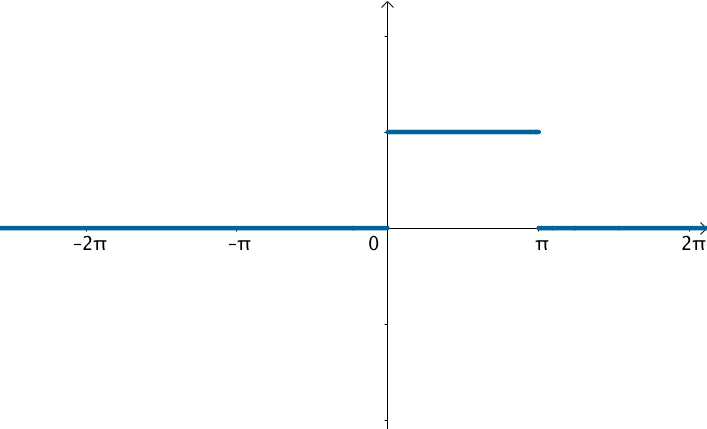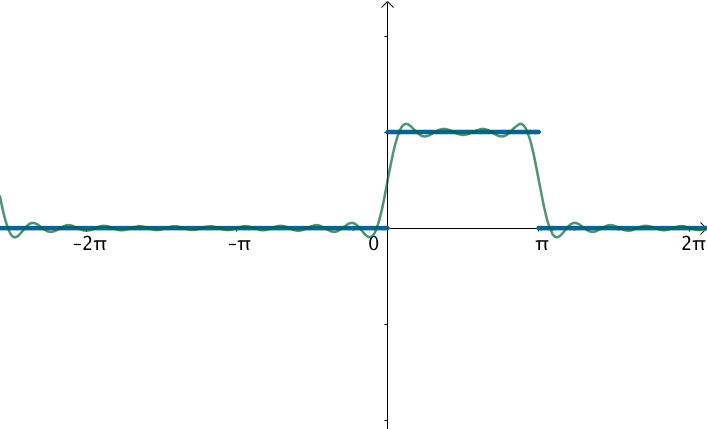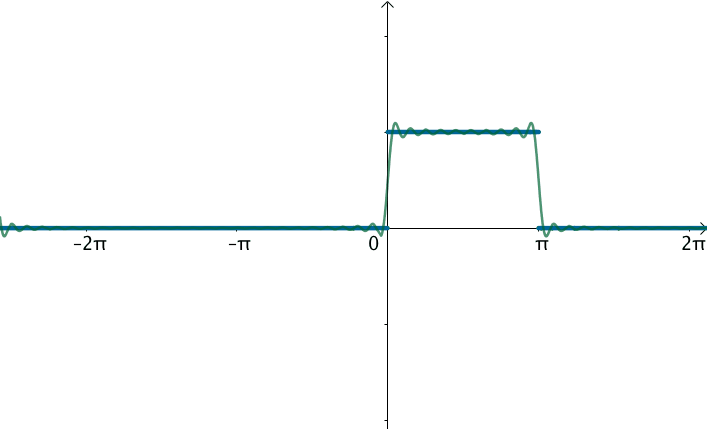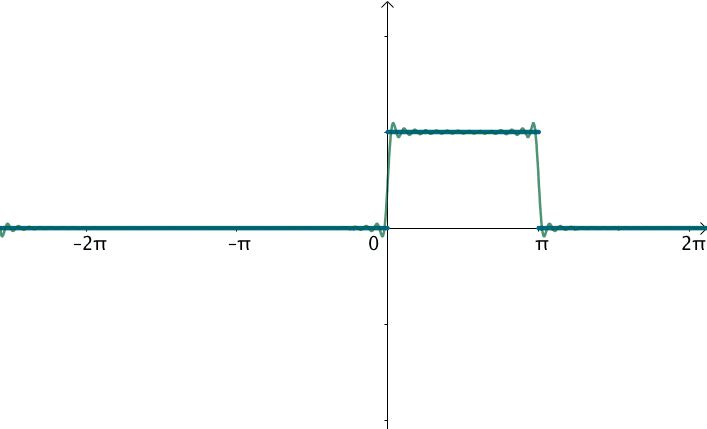
观察下频域,之前说了,对于周期为 T 的函数 f(x),其基为 $$ { 1, \cos(\frac{2\pi n}{T}x), \sin(\frac{2\pi n}{T}x)} $$ 刚才举例的方波 T=2π,对应的基就为 $$ { 1, \sin(x), \sin(2x), \sin(3x), \sin(4x), \sin(5x) \dots \sin(nx) } $$ 对应的频率 $$ { 0 Hz, 1Hz, 2Hz, 3Hz, 4Hz \dots nHz } $$ 当方波的 T 不断增大,这些频率越来越集中:
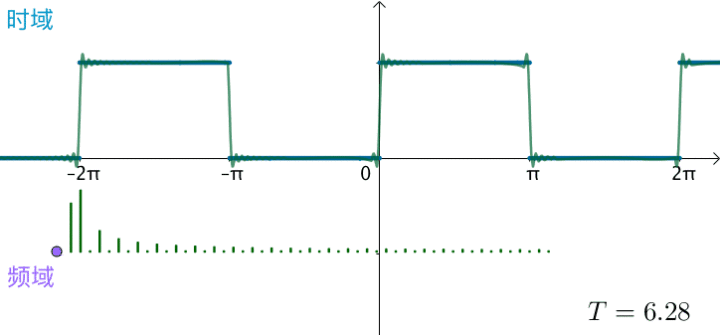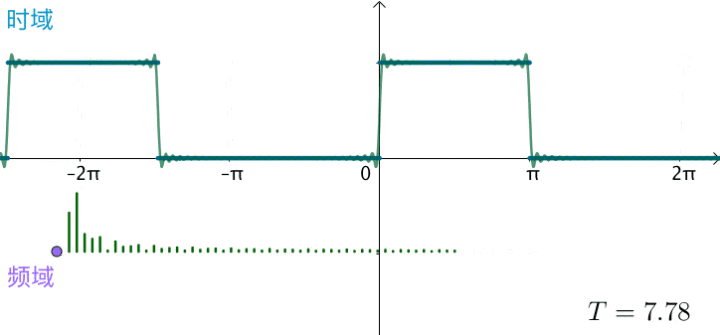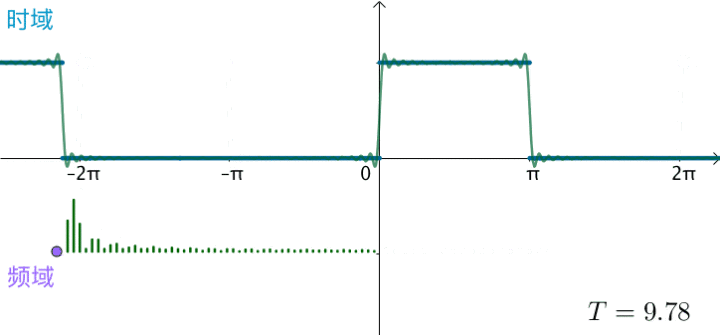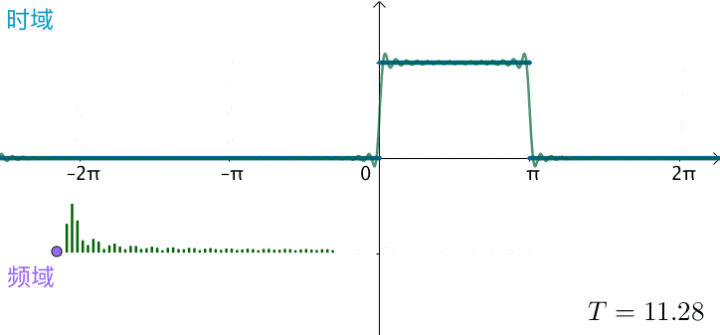
当 $ T = 2\pi \Rightarrow T = \infty $,这些频率就会变得稠密,直至连续,变为一条频域曲线:
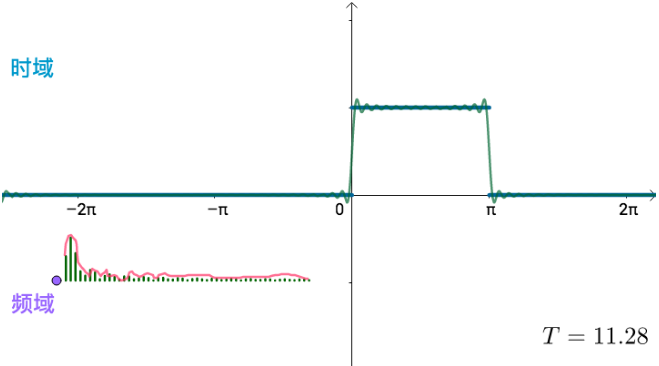
时域的信号周期越长,那么频域就越集中,越不容易发生混叠,越容易抽象出时间信号的周期性重复信息,此时自然而然的,周期性这个词就出现了。
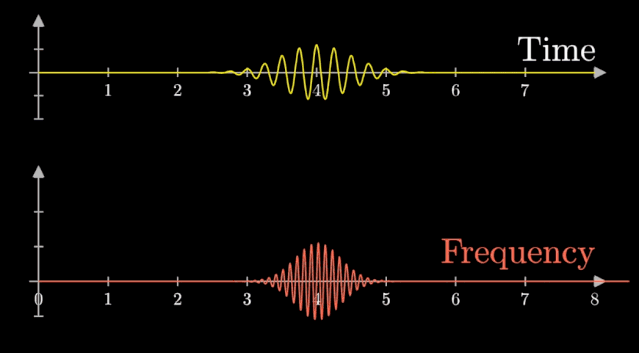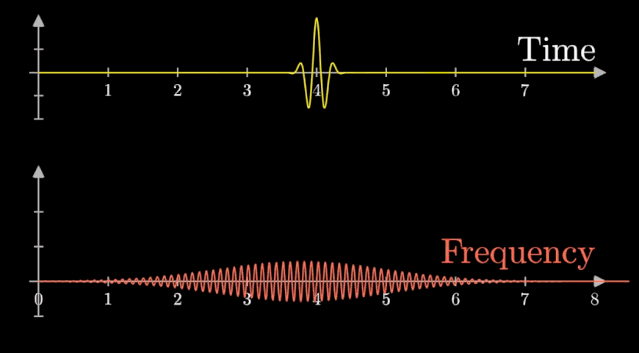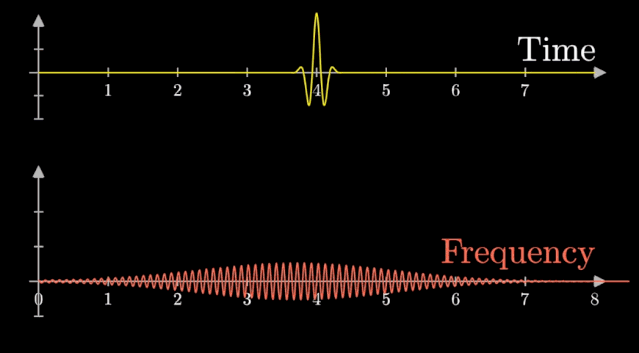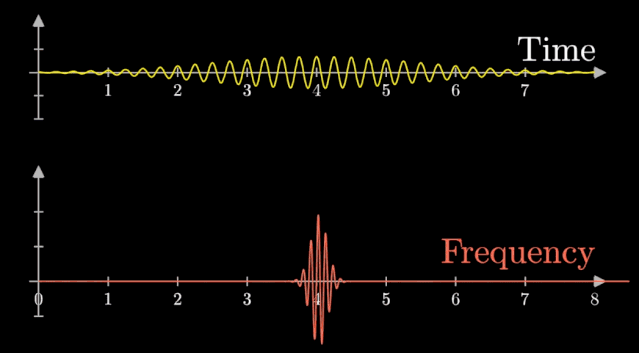
这就是傅里叶变换,让$ T = \infty $ ,上面这根频率曲线。
将一个时域非周期的连续信号,转换为一个非周期连续信号。
| 从傅里叶级数到傅里叶变换 | |
|---|---|
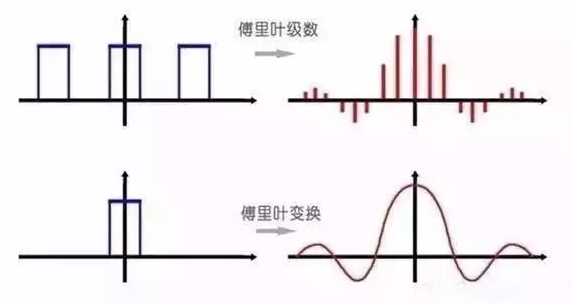 | 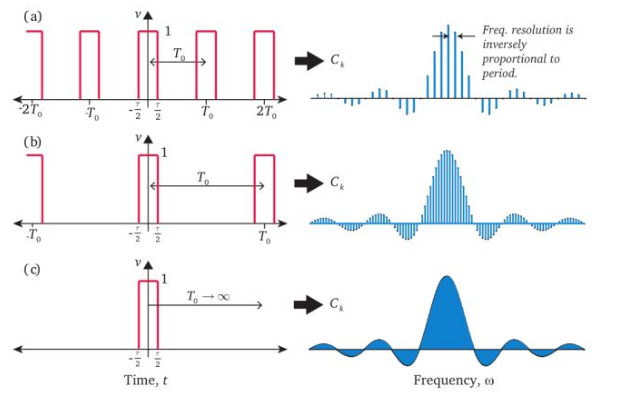 |
| · 周期函数,可以通过傅立叶级数画出频域图 · 增长周期,频域图变得越来越密集 · T=∞,得到傅立叶变换,频域图变为连续的曲线 |
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
所以说,钢琴谱其实并非一个连续的频谱,而是很多在时间上离散的频率,但是这样的一个贴切的比喻真的是很难找出第二个来了。
因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?
# 你见过大海么?
为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。
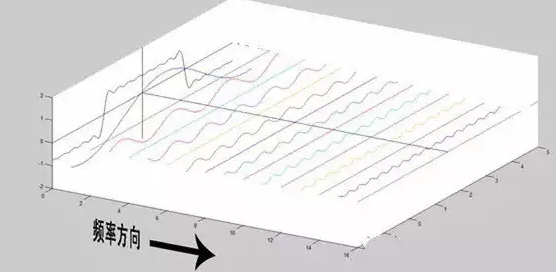
以上是离散谱,那么连续谱是什么样子呢?
尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续……
直到变得像波涛起伏的大海:

很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。
不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
| 傅里叶变换 | 傅里叶逆变换 |
|---|---|
不过,这个故事还没有讲完,接下去,我保证让你看到一幅比上图更美丽壮观的图片,但是这里需要介绍到一个数学工具才能然故事继续,这个工具就是——欧拉公式
# 指数形式的傅里叶变换
有了欧拉公式的帮助,我们便知道:
- 正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。
- 而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?
# 光波
高中时我们就学过,自然光是由不同颜色的光叠加而成的,而最著名的实验就是牛顿师傅的三棱镜实验:
所以其实我们在很早就接触到了光的频谱,只是并没有了解频谱更重要的意义。
但不同的是,傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从0到无穷所有频率的组合。
这里,我们可以用两种方法来理解正弦波:
第一种前面已经讲过了,就是螺旋线在实轴的投影。
另一种需要借助欧拉公式的另一种形式去理解:
欧拉公式x分别取t和-t:
- eit = cos(t) + i sin(t)
- e- it = cos(t) - i sin(t)
- 将以上两式相加再除2,得到:cos(t) = (eit + e- it) / 2
如何理解?
eit可以理解为一条逆时针旋转的螺旋线,那么e- it 则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
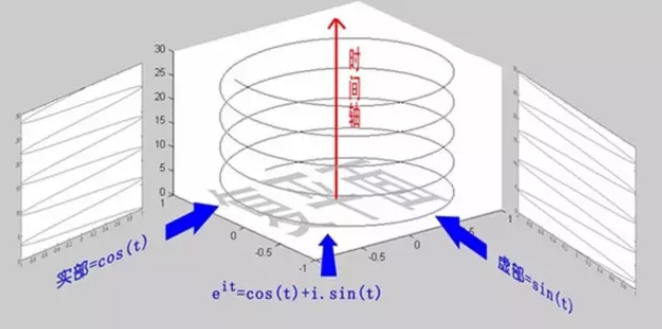
举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。
这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
好了,刚才我们已经看到了大海——连续的傅里叶变换频谱,现在想一想,连续的螺旋线会是什么样子:
想象一下再往下翻:

# 是不是很漂亮?
# 你猜猜,这个图形在时域是什么样子?
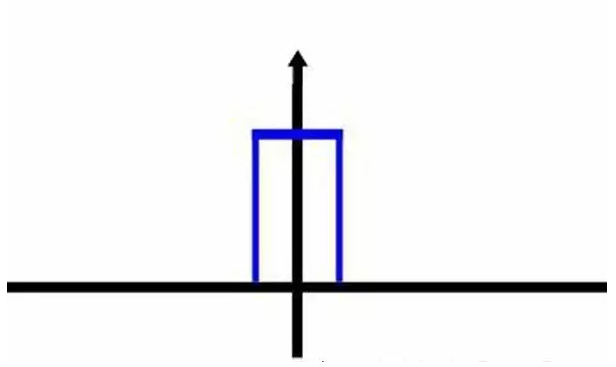
哈哈,是不是觉得被狠狠扇了一个耳光。数学就是这么一个把简单的问题搞得很复杂的东西。
顺便说一句,那个像大海螺一样的图,为了方便观看,我仅仅展示了其中正频率的部分,负频率的部分没有显示出来。
如果你认真去看,海螺图上的每一条螺旋线都是可以清楚的看到的,每一条螺旋线都有着不同的振幅(旋转半径),频率(旋转周期)以及相位。而将所有螺旋线连成平面,就是这幅海螺图了。
非周期信号f(t)可以看成是周期T→∞的周期信号。当T趋于无穷大时,角频率Ω会趋于无穷小,因此信号的频谱会变成连续谱,各频率分量的幅度也趋于无穷小。不过,这些无穷小量之间也有差别。
为此我们引入频谱密度的概念,即
考虑到Ω趋于无穷小,因此Ω记为dw,nΩ记为w,则
这也是傅里叶变换公式,我们将求和变成积分符号可以得到反傅里叶变换公式即
这样周期信号的离散频谱就过度到非周期信号的连续频谱。


