欧拉公式

欧拉公式

欧拉公式，被誉为上帝公式，$e$、$i$ 、$\pi$ 、乘法单位元1、加法单位元0，这五个重要的数学元素全部被包含在内，在数学爱好者眼里，仿佛一行诗道尽了数学的美好。

宇宙耍帅第一公式：欧拉公式

欧拉公式将指数函数的定义域扩大到了复数域，建立和三角函数和指数函数的关系，被誉为“数学中的天桥”。形式简单，结果惊人，欧拉本人都把这个公式刻在皇家科学院的大门上，看来必须好好推敲一番。

• 世界上最完美的公式—欧拉公式，也称上帝公式。据说，里面包含着上帝的创世秘密。
• e：自然对数，代表大自然
• i：虚数单位，代表思想
• π：圆周率，代表无限
• 1：代表起点
• 0：代表终点

合起来读就是

化整为零

欧拉公式就是一根木头连续旋转一圈就会得到一个圆。

欧拉公式与旋转

虚数i这个概念大家在高中就接触过，但那时我们只知道它是-1的平方根，可是它真正的意义是什么呢?

虚数i的几何意义——旋转
这里有一条数轴，数轴上有一红色线段，长度为1 当它乘以3的时候，它的长度发生了变化，变成了蓝色的线段 而当它乘以-1的时候，就变成了绿色的线段或者说线段在数轴上围绕原点旋转了180度。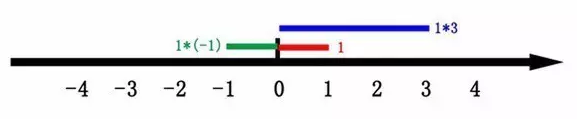
我们知道乘-1其实就是乘了两次 i ，使线段旋转了180度，那么乘一次 i 呢？ ——答案很简单——旋转了90度。 同时，我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面，也称复平面。 这样我们就了解到，乘虚数 i 的一个功能——旋转。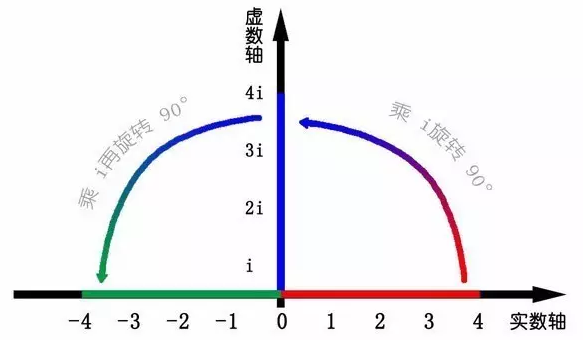

另外，e^t是什么样呢？

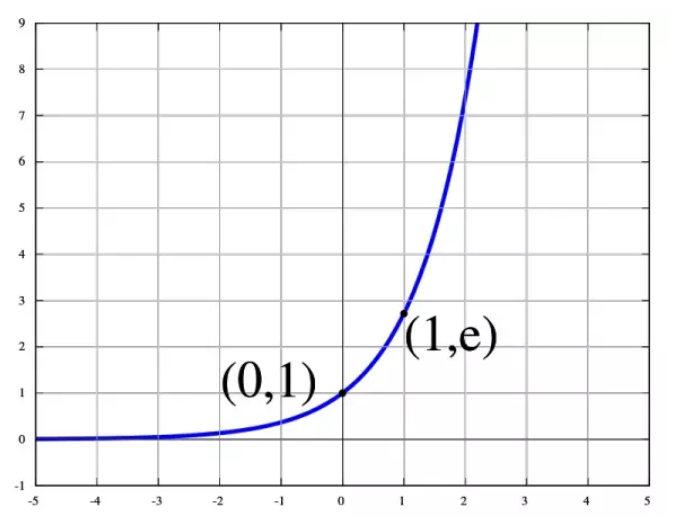
但当你在指数上加上i之后呢？变成了一个螺旋线。是不是和电磁场很像？

现在，就有请宇宙第一耍帅公式欧拉公式隆重登场——

$e^{\imath \theta} = \cos \theta + \imath \sin \theta$

这个公式在数学领域的意义要远大于傅里叶分析，但是称它为宇宙第一耍帅公式是因为它的特殊形式——当 $\theta$ 等于 $\pi$ 的时候。

$e^{\imath \pi} + 1 = 0$

经常有理工科的学生为了跟妹子表现自己的学术功底，用这个公式来给妹子解释数学之美：”石榴姐你看，这个公式里既有自然底数e，自然数1和0，虚数i还有圆周率pi，它是这么简洁，这么美丽啊！“但是姑娘们心里往往只有一句话：”臭屌丝……“

这个公式关键的作用，是将正弦波统一成了简单的指数形式。

指数函数（逆操作对数函数同理）是加法和乘法运算的桥梁，在自变量包含复数时表示旋转。

举例：

$\large e^{\pi i}$表示的是在单位圆上逆时针在旋转180°这个变换。

我们来看看图像上的涵义：

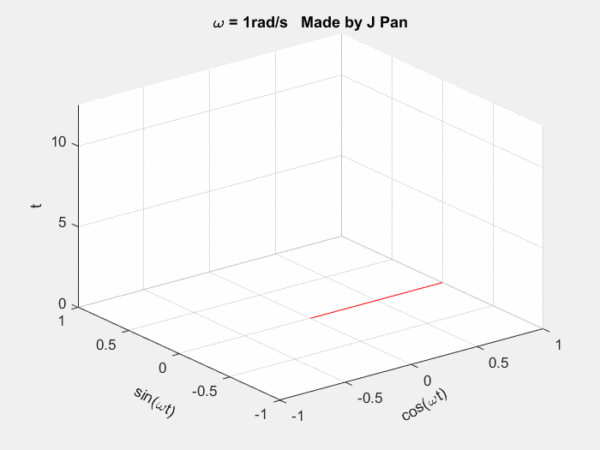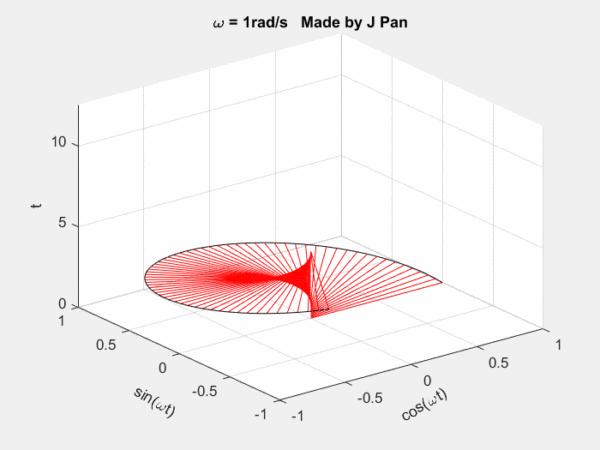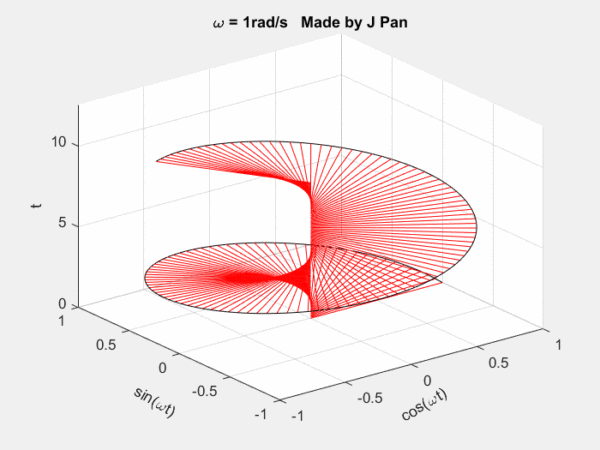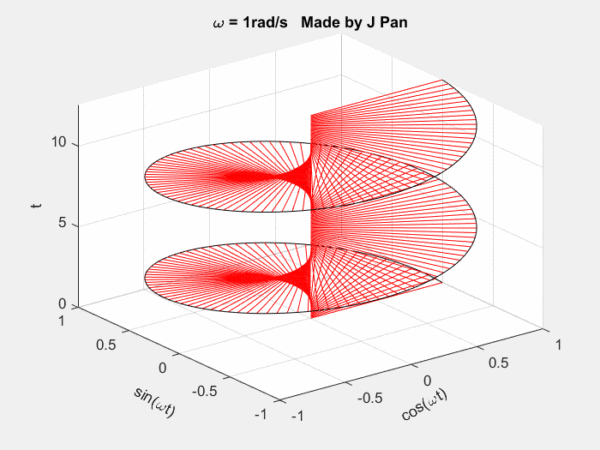
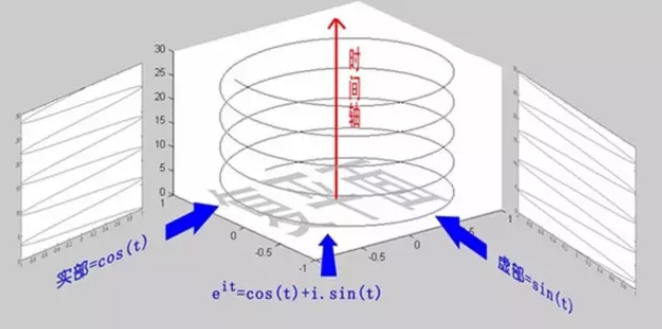
欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。

• 如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。
• 而右侧的投影则是一个正弦函数。

当然，更重要的意义在于复数运算保留了二维信息。

假如我让你计算3+5，虽然你可以轻松的计算出8，但是如果让你分解8你会有无数种分解的方法，3和5原始在各自维度上的信息被覆盖了。 但是计算3+5i的话，你依然可以分解出实部和虚部，就像上图那样。

基于以上两个理由，用复数来描述电场与磁场简直完美到爆棚！ 我们即可以让电场强度与复数磁场强度相加而不损失各自的信息，又满足了电场与磁场90度垂直的要求。另外，一旦我们需要让任何一个场旋转90度，只要乘一个“i”就可以了

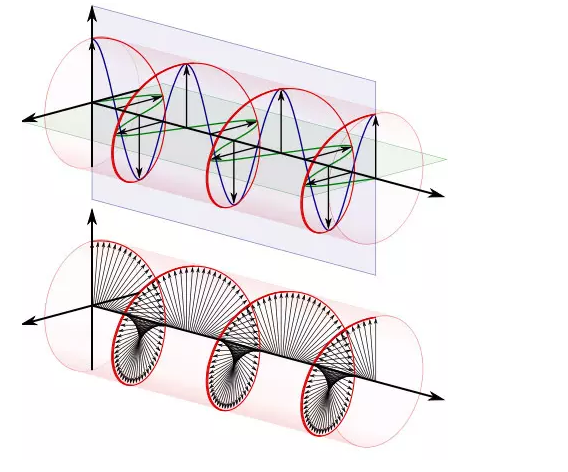
欧拉公式在形式上很简单，是怎么发现的呢？

1. 欧拉公式与泰勒公式

欧拉最早是通过泰勒公式观察出欧拉公式的

$\Large e^x = 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + ... $

将 $x= \imath \theta$ 代入 $e$ 可得， $\Large e^{\imath \theta} = 1 + \imath \theta + \frac{1}{2!} (\imath \theta)^2 + \frac{1}{3!} (\imath \theta)^3 + \frac{1}{4!} (\imath \theta)^4 = \cos \theta + \imath \sin \theta$

..........

2. 欧拉公式与三角函数

根据欧拉公式 $\Large e^{\imath \theta} = cos \theta + \imath sin \theta$

$sin \theta = \frac{e^{\imath \theta} - e^{-\imath \theta}}{2 \imath}$

$cos \theta = \frac{e^{\imath \theta} + e^{-\imath \theta}}{2 \imath}$

三角函数定义域被扩大到了复数域。

3. 欧拉恒等式

当 $\theta = \pi$ 的时候，代入欧拉公式：

$\Large e^{\imath \pi} = cos \pi + \imath sin \pi = -1 \Rightarrow e^{\imath \pi} + 1 = 0$

$\Large e^{\imath \pi} + 1 = 0$ 就是欧拉恒等式，被誉为上帝公式