傅里叶级数的三角函数分解的代数推导

傅里叶级数用三角函数分解的代数推导

傅里叶级数

傅里叶级数的公式

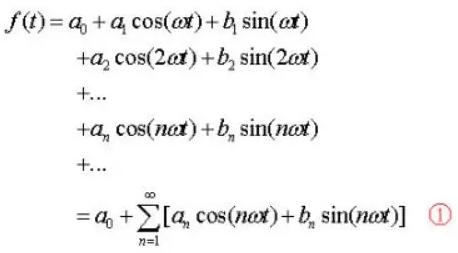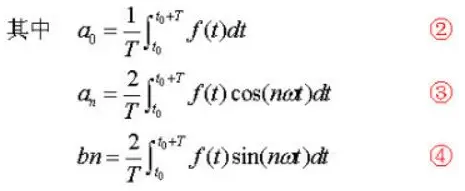数学推导

步骤	过程
原始函数 完整形式
每一项 乘以cos2x 从[-π, π]积分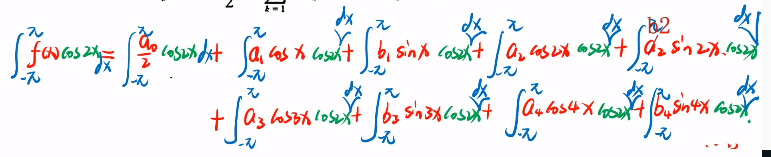
由于三角函数正交特性 消去大量0项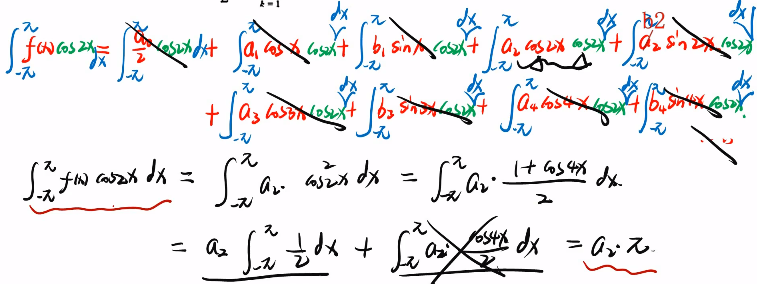
获得a2的值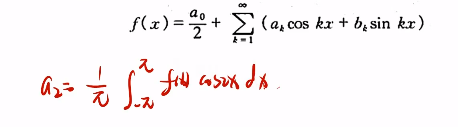

同理，要获得b₄的值，都 × sin4x

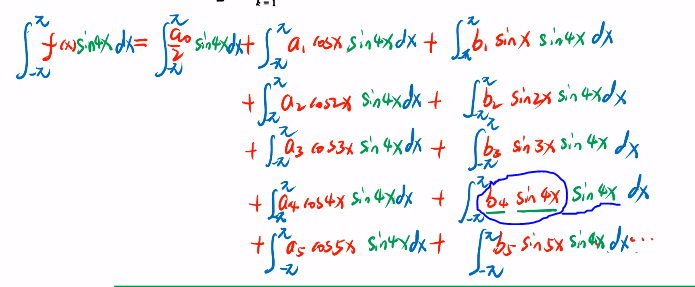
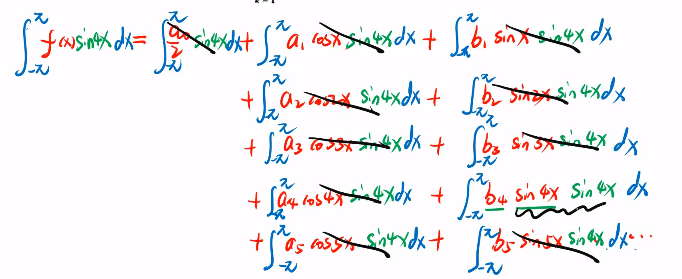
从而得到b₄的值

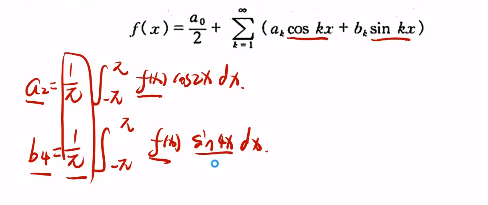
基于以上内容，我们可以获得规律：

事实上，如果能够写出①式，不难求出各个系数的表达式，关键是人们不会想到一个周期函数竟然可以用一些简单的正弦或余弦函数来表达，且这个表达式是一个无穷级数。这当然就是数学家傅里叶的天才之作了，我等只有拼命理解的份了。

傅里叶级数的产生过程可以分为以下三步：

1、设想可以把一个周期函数f(t)通过最简单的一系列正弦函数来表示，即5式;

2、通过变形后用三角级数(含sin和cos)来表示;

3、通过积分，把各未知系数用f(t)的积分式来表达;

4、最后得到的4个表达式就是傅里叶级数公式。

参考资料

https://www.bilibili.com/video/BV1c741127cy?from=search&seid=17844535962260850517