傅里叶级数的指数形式

傅里叶级数的三角函数形式

$\Large f(x) = \frac{a_0}{2} + \sum^{\infty}_{n=1}(a_n\cos(nx) + b_n \sin(nx))$

$\Large f(x) = C + \sum^{\infty}_{n=1} \bigg(a_n\cos(\frac{2\pi n}{T}x) + b_n \sin(\frac{2\pi n}{T} x) \bigg) C \in \mathbb{R}$

周期函数的傅里叶级数

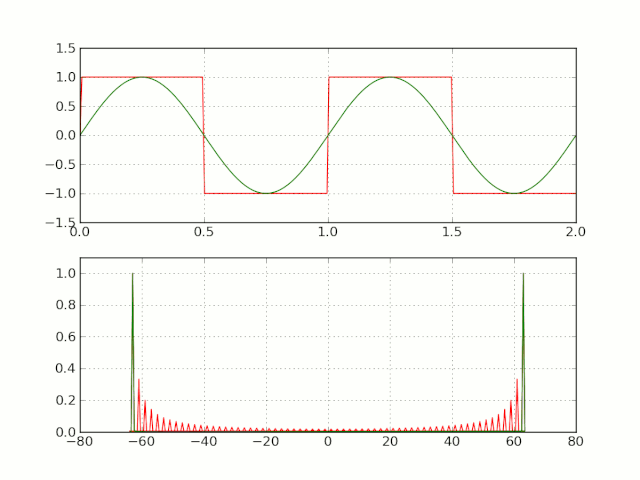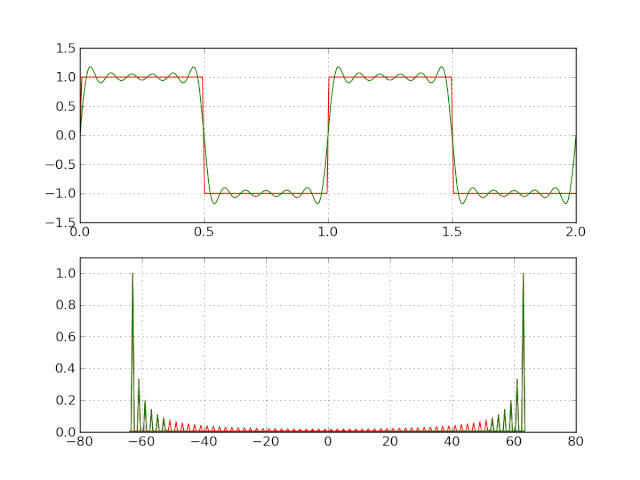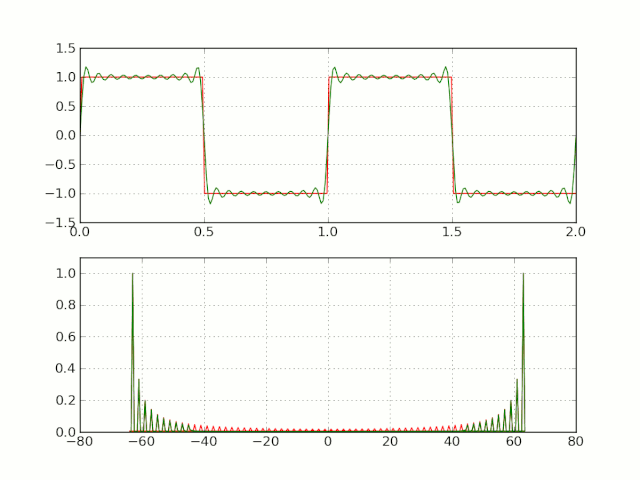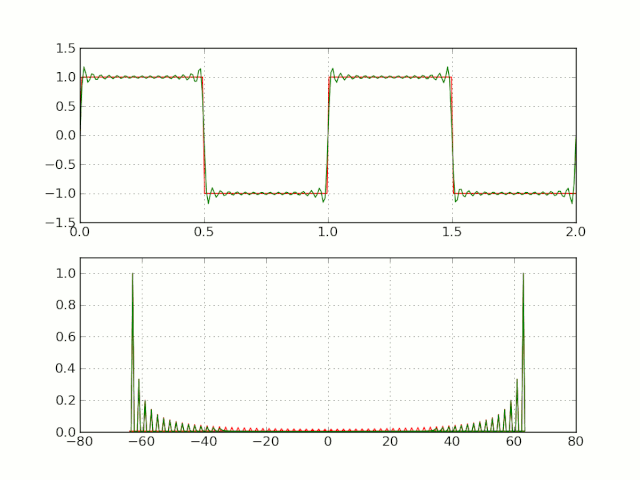
三角形式的傅里叶级数，含义比较明确，但是运算不是很方便。（因而经常采用指数形式的傅里叶级数）

傅里叶变换还有一种复频域的表示方式，通过复频域表示更加简单直观，但这就需要用到大名鼎鼎的欧拉公式。

知识补充：欧拉公式

利用欧拉公式可以将信号分解到复指数域上，即

$复频域傅里叶级数$

其中，

任意周期信号都可以分解成不同频率的虚指数信号之和。各个信号分量随时间t的变化规律都是一样的，差别仅仅是幅度、频率和相位不同。因此可以用一根线段来表示某个分量的幅度或者相位，用线段的位置表示相应的频率。这也分别称为幅度谱和相位谱。

傅里叶级数的指数形式

但是为了能更好的理解指数形式的傅里叶级数，我们还需要一个工具来帮忙——欧拉公式。

引入$\Large e^{\imath wt}$

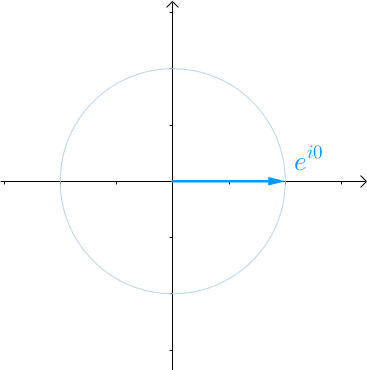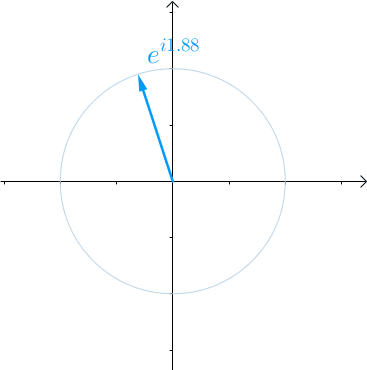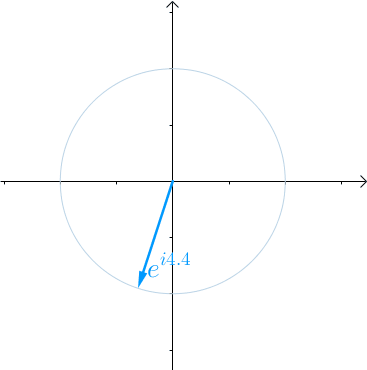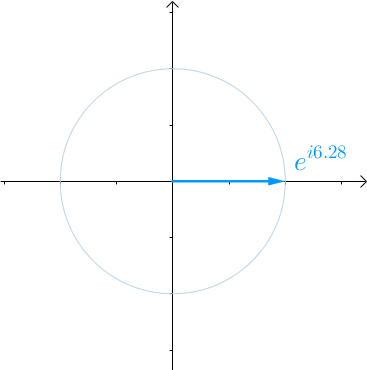
看到复数不要怕，根据之前的文章《欧拉公式》，对任意实数x，都存在 $\Large e^{\imath \theta} = cos (\theta) + \imath sin (\theta)$ ，$\Large \imath$ 是虚数单位。看到类似于 $e^{i\theta}$ 这种就应该想到复平面上的一个夹角为 $\theta$ 的向量：

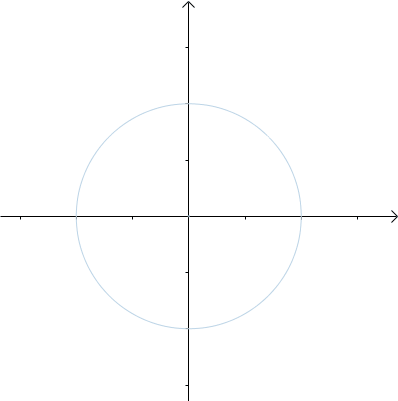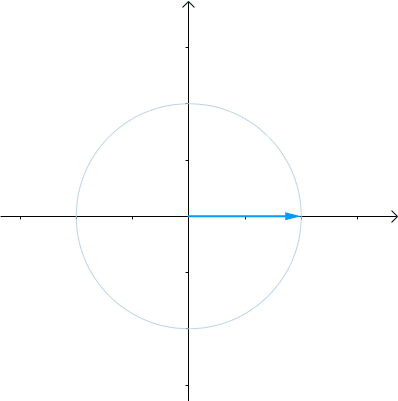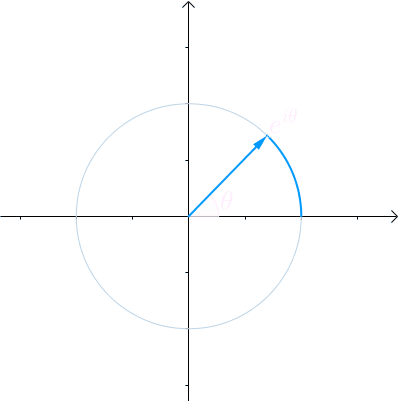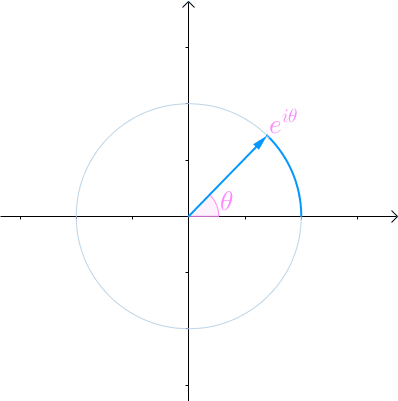
那么当 $\theta$ 不再是常数，而是代表时间的变量t的时候：

$\Large e^{\imath \theta} \longrightarrow e^{\imath t}$

随着时间t的流逝，从0开始增长，这个向量就会旋转起来，$2\pi$ 秒会旋转一圈，也就是$ T=2\pi$：

通过$\Large e^{i\omega t}$表示$\Large \sin(t)$

欧拉公式

$\Large e^{\imath \pi} + 1 = 0$

$\Large e^{\imath \theta} = cos \theta + \imath sin \theta$

根据欧拉公式，有：

$\Large e^{\imath t} = cos (t) + \imath sin (t)$

所以，

举例说明	图示
在时间t轴上 把$\Large e^{it}$向量的虚部（也就是纵坐标）记录下来 得到的就是$\Large \sin(t)$
在时间t轴上 把$\Large e^{i2t}$向量的虚部（也就是纵坐标）记录下来 得到的就是$\Large 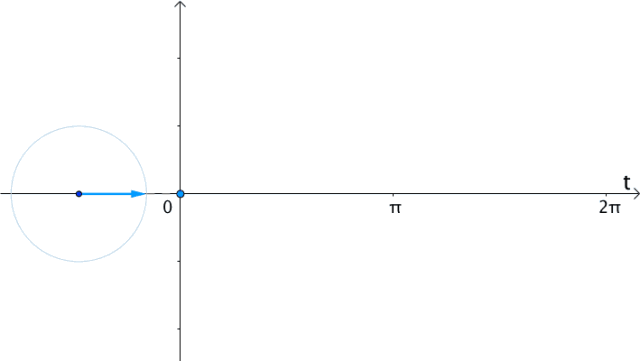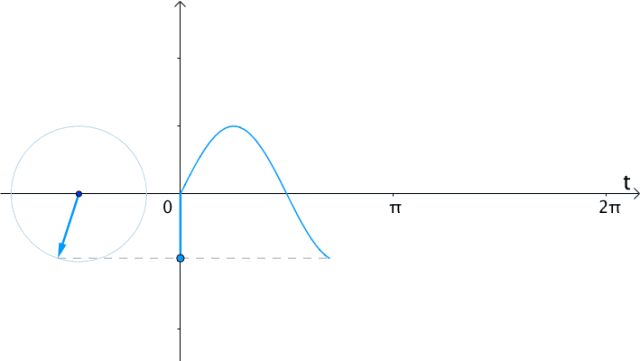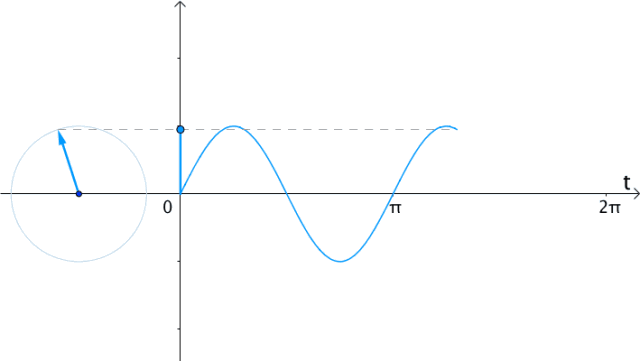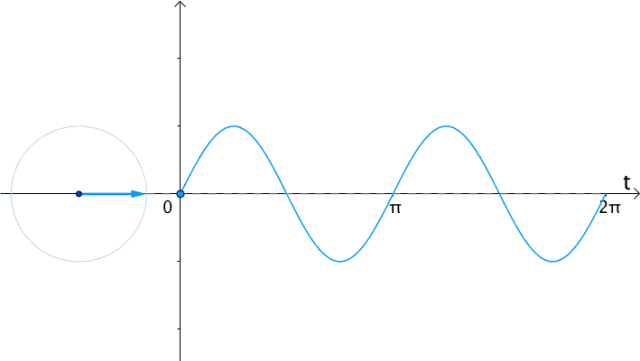\sin(2t)$
在时间t轴上 把$\Large e^{it}$的实部（横坐标）记录下来 得到的就是的$\Large \c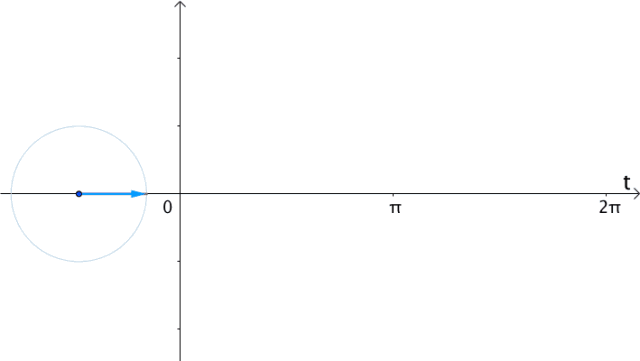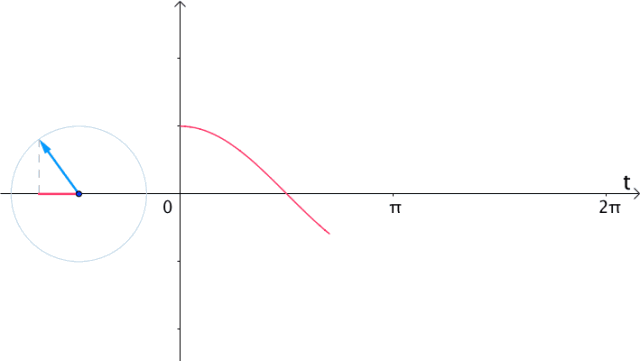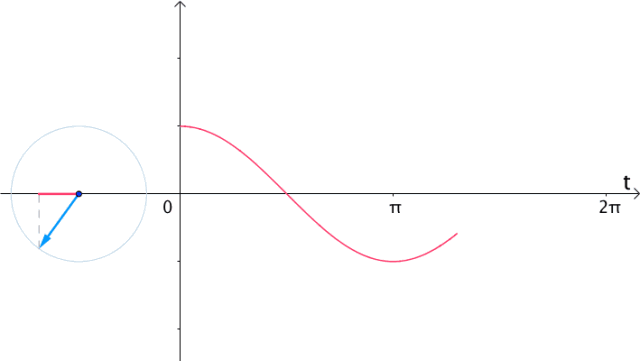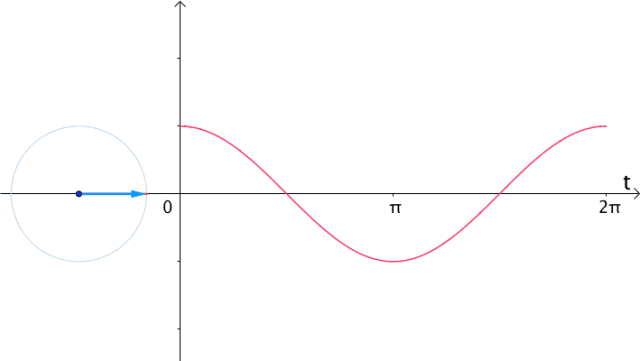os(t)$曲线

更一般的，具有两种看待$sin(x),cos(x)$的角度： $$ \Large e^{i\omega t} \Leftrightarrow \begin{cases} \sin(\omega t)\ \cos(\omega t) \end{cases} $$

这两种角度，一个可以观察到旋转的频率，所以称为频域；一个可以看到流逝的时间，所以称为时域：

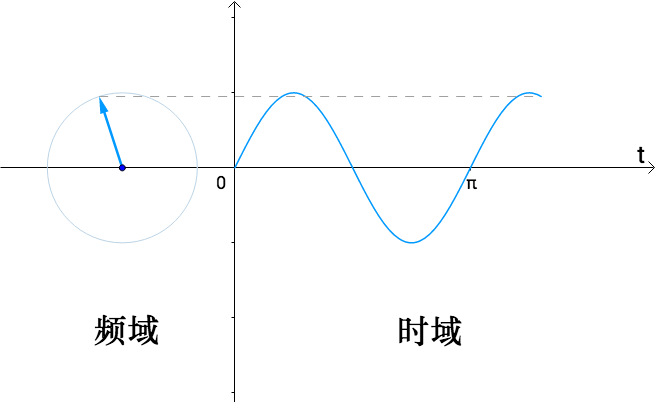
因此，我们可以推出 $ \cos x, \sin x$ 可表示成

$\Large \cos x = \frac{e^{\imath x} + e^{-\imath x}}{2}$

$\Large \sin x = \frac{e^{\imath x} - e^{-\imath x}}{2\imath}$

根据上式，我们可以写出傅立叶级数的另外一种形式，这种复数形式也是向量：

$\Huge f(x) = \sum^{\infty}_{n = -\infty} \underbrace{c_n}_{基的坐标} · \underbrace{e^{\imath \frac{2\pi nx}{T}}}_{正交基}$

其中

将以上的$f(x)$扩展，可以写作：

$\Large f(x)=\cdots+c_{-1}e^{(-1)\cdot ix}+c_{0}e^{(0)\cdot ix}+c_{1}e^{(1)\cdot ix}+c_{2}e^{(2)\cdot ix}+\cdots$

因为{$e^{inx}$}，$n \in \mathbb{N}$ 是基，所以可把$f(x)$表示为一个向量：

$\Large f(x)=(\cdots, c_{-1}, c_0, c_1, c_2, \cdots)$

这个向量其实就是傅立叶级数的向量。

因为基{$e^{inx}$}，$n \in \mathbb{N}$ 实际上反映了周期运动的频率，我们以频率为基，所以这样看待傅立叶级数的方式就是“频域”。

如何形象的理解

根据第一部分内容，我们已知类似于 $e^{i\theta}$ 这种会想到复平面上的一个夹角为 $\theta$ 的向量。

实际上就是说，$f(x)$，曲线可以理解为无数旋转的叠加

这怎么理解呢？看下面的例子。

火星的轨迹曲线

地球上观察到的火星运行的轨迹	通过两个圆周运动的叠加来模拟出这个曲线

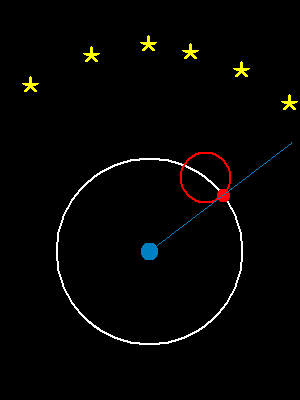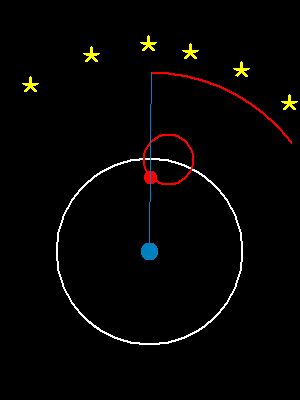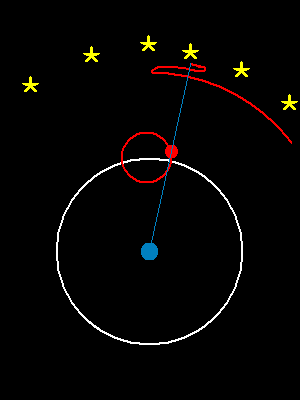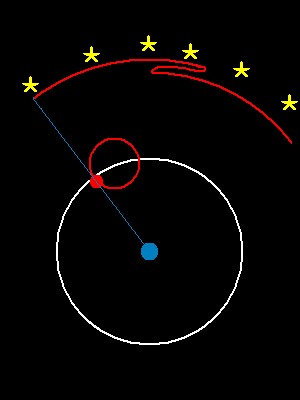其实这就是地心说，感兴趣可以看下“爱因斯坦和牛顿是否被严重高估了？”。

通过这种圆环套圆环的做法，可以模拟各种复杂的图形，比如可以画出辛普森。 注（多圆环嵌套画出辛普森）

YouTube地址

腾讯视频地址

旋转的傅立叶

所以，傅立叶级数实际上就是把$f(x)$或$f(t)$看作是圆周运动的组合。

只是 $x$ 或者 $t$ 是不断变大的，而不是绕着圆变换的，所以就画出了函数曲线：

不断增大的 $x$ 或者$t$ 就好像是时间流逝，永不回头，所以也称为“时域”。

傅立叶级数的不同形式

	傅立叶级数形式
三角函数形式	$\Large f(x) = C + \sum^{\infty}_{n=1} \bigg(a_n\cos(\frac{2\pi n}{T}x) + b_n \sin(\frac{2\pi n}{T} x) \bigg) C \in \mathbb{R}$
指数形式	$\Large f(x) = \sum^{\infty}_{n = -\infty} \underbrace{c_n}_{基的坐标} · \underbrace{e^{\imath \frac{2\pi nx}{T}}}_{正交基}$

---

于是得到了傅里叶变换就是

$\Large F(\omega) = \int^{+\infty}_{-\infty} f(x)e^{-\imath \omega x}dx$